Oblique Prisms
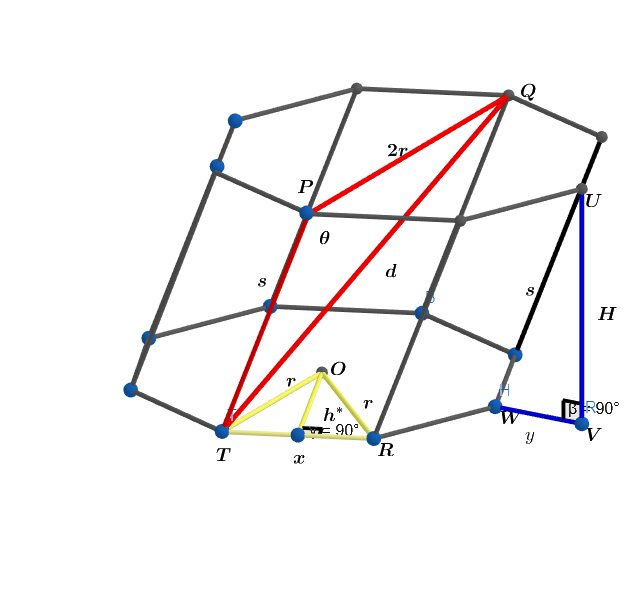
Let the above Oblique Octagonal Prism be an analogy of a -gonal Oblique Prism.
In the above Oblique Octagonal Prism and is a right triangle.
Extending to a -gonal Oblique Prism let the volume and the lateral surface area of the Oblique -gonal Prism be and respectively.
(1): Find the side of the -gon which maximizes the distance .
(2): Show is independent of and find the distance and find (in degrees).
(3): Find .
(4): Check your results in (2) and (3) using a oblique cylinder.
Express the answer as .
Note: In the above diagram and
:
The answer is 148.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 x = r sin ( 4 n π ) ⟹ r = 2 sin ( 4 n π ) x ⟹ h ∗ = 2 x cot ( 4 n π ) ⟹ the area of the 4 n -gon A = n x 2 cot ( 4 n π ) .
The volume V = n x 2 cot ( 4 n π ) H = 1 ⟹ H = n x 2 tan ( 4 n π )
The lateral surface area S = 4 n x s = 1 ⟹ s = 4 n x 1 ⟹ Y ( r ) = y 2 ( r ) = s 2 − H 2 = n 2 1 ( 1 6 x 2 1 − x 4 tan 2 ( 4 n π ) ) ⟹
d r d Y = 8 n 2 x 5 3 2 tan 2 ( 4 n π ) − x 2 = 0 ⟹ x = 4 2 tan ( 4 n π ) ⟹ r = 2 2 sec ( 4 n π ) , s = 1 6 2 n cot ( 4 n π ) , H = 3 2 n cot ( 4 n π ) and y = s 2 − H 2 = 3 2 n cot ( 4 n π ) = H .
Note: d x 2 d 2 Y ∣ x = 4 2 tan ( 4 n π ) = ( 8 n 2 ( 4 2 tan ( 4 n π ) ) 4 1 ) ( 3 − 5 cot ( 4 n π ) ) < 0 , since cot ( 4 n π ) ≥ 1 and is increasing for increasing n ⟹ we have a max at x = 4 2 tan ( 4 n π )
Let m ∠ U W V = λ ⟹ cos ( λ ) = s y = 2 1 and θ = 1 8 0 − λ ⟹ cos ( θ ) = cos ( 1 8 0 − λ ) = − cos ( λ ) = 2 − 1 ⟹ θ = 1 3 5 ∘
r = 2 2 sec ( 4 n π ) and s = 1 6 2 n cot ( 4 n π ) ⟹
d 2 ( n ) = s 2 + 4 r 2 + 4 r s cos ( λ ) = 2 9 ( n sin ( 4 n π ) ) 2 cos 2 ( 4 n π ) + cos 2 ( 4 n π ) 2 5 + 2 2 ( n sin ( 4 n π ) ) 1 ⟹
d n = 2 9 ( n sin ( 4 n π ) ) 2 cos 2 ( 4 n π ) + cos 2 ( 4 n π ) 2 5 + 2 2 ( n sin ( 4 n π ) ) 1
Using the inequality cos ( x ) < x sin ( x ) < 1 ⟹ 4 π cos ( 4 n π ) < n sin ( 4 n π ) < 4 π ⟹
lim n → ∞ d n = 3 2 π 2 1 + 3 2 + π 2 = 4 2 π 3 2 2 π 2 + 3 2 2 π + 1 ≈ 5 . 6 9 6 7 8
For n = 1 d 1 = 1 6 1 2 2 1 5 + 2 8 + 1 ≈ 8 . 0 3 1 3 1
∴ ⌊ d + θ + d 1 ⌋ = 1 4 8 .
Checking using oblique cylinder:
In the above Oblique Cylinder m ∠ Q P T = θ , T P Q U is a parallelogram and △ P R T is a right triangle.
V = π r 2 H = 1 ⟹ H = π r 2 1 and A = 2 π r s = 1 ⟹ s = 2 π r 1
⟹ Y ( r ) = y 2 ( r ) = s 2 ( r ) − H 2 ( r ) = 4 π 2 r 2 1 − π 2 r 4 1 ⟹ d r d Y = π 2 1 ( 2 r 5 8 − r 2 ) r > = 0 ⟹ r = 2 2 ⟹ s = 4 2 π 1 and H = 8 π 1 and y = s 2 − H 2 = 8 π 1 = H .
d r 2 d 2 Y ∣ r = 2 2 = ( 8 π ) 2 − 1 < 0 ⟹ max at r = 2 2 .
Let m ∠ P T R = λ ⟹ cos ( λ ) = s ( r ) y ( r ) = 2 1 and θ = 1 8 0 − λ ⟹ cos ( θ ) = c o s ( 1 8 0 − θ ) = − c o s ( λ ) = − 2 1 ⟹ θ = 1 3 5 ∘
⟹ d 2 = s 2 + 4 r 2 + 4 r s cos ( λ ) = 3 2 π 2 1 + 3 2 + π 2 = 3 2 π 2 3 2 2 π 2 + 3 2 2 π + 1 ⟹ d = 4 2 π 3 2 2 π 2 + 3 2 2 π + 1 ≈ 5 . 6 9 6 7 8
Note: Using the above x = 4 2 tan ( 4 n π ) ⟹ r = 2 2 sec ( 4 n π ) , s = 1 6 2 n cot ( 4 n π ) , and y = 3 2 n cot ( 4 n π ) = H we obtain:
r = lim n → ∞ r n = 2 2 , y = lim n → ∞ 3 2 ( n sin ( 4 n π ) ) cos ( 4 n π ) = 8 π 1 = H , and s = lim n → ∞ 1 6 2 ( n sin ( 4 n π ) ) cos ( 4 n π ) = 4 2 π 1