Oblique Square Pyramid
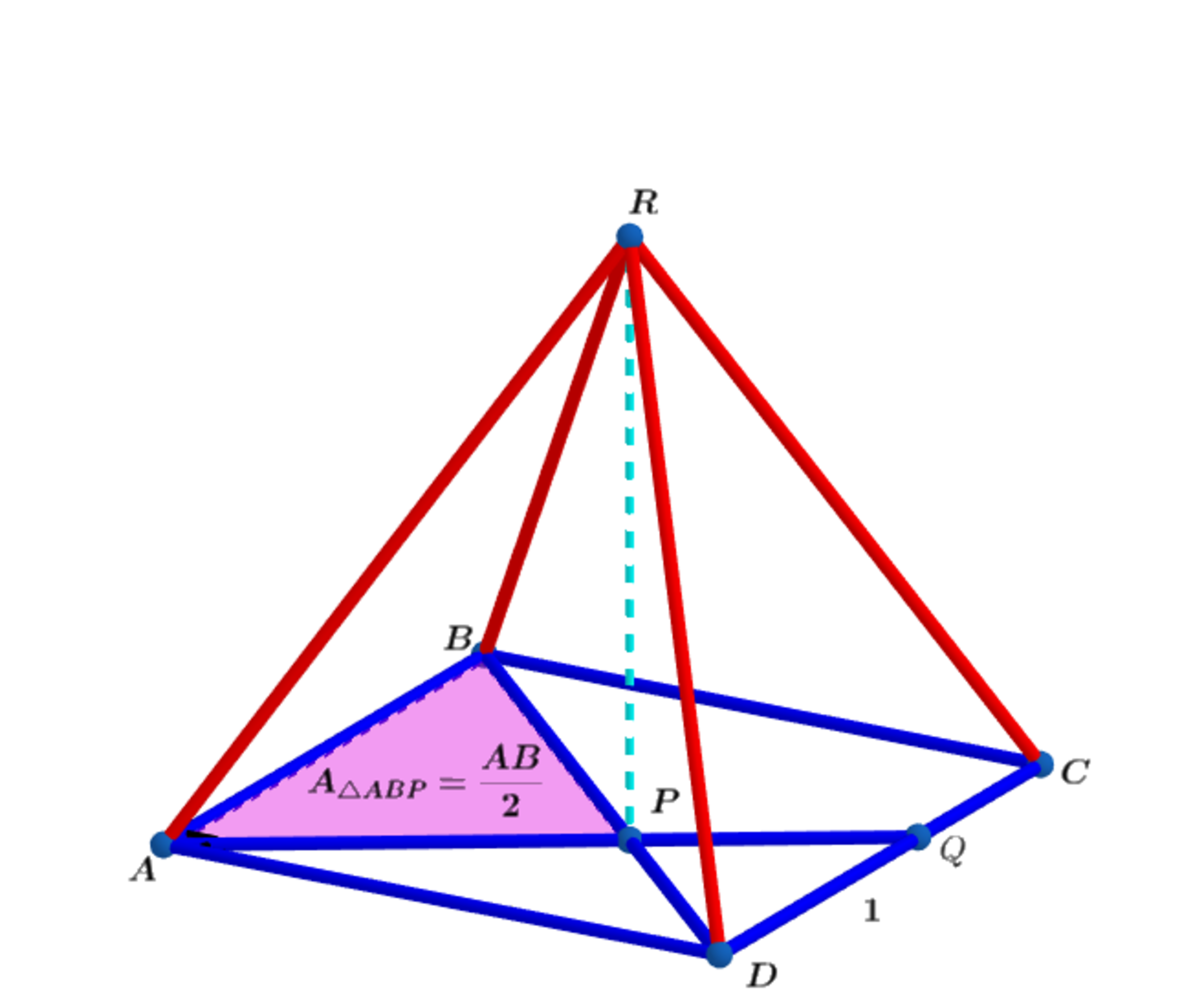
In square base A B C D , B D and A Q intersect at P with Q D = 1 and the area
A △ A B P = 2 A B .
Erect a normal at P so that the height P R of the oblique square pyramid above is A B .
Let S be the lateral surface area of the above pyramid.
If P R S = α ϕ + β , where α and β are coprime positive integers and ϕ is the
golden ratio, find α + β .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I got the answer in terms of the golden ratio as P R S = Φ 2 + ( Φ − 1 ) 2 + 1 + Φ 2 , and left it there!
I would have liked to do that, but I needed a numerical answer for brillant.
I provided two solutions for the square base.
Solution using coordinate geometry:
For B D : y = a − x and for A Q : y = a 1 x ⟹ x = a + 1 a 2 ⟹
A △ A B P = 2 ( a + 1 ) a 3 = 2 a ⟹ a ( a 2 − a − 1 ) = 0 a > 0 ⟹
a = 2 1 + 5 = ϕ and P : ( 1 , ϕ − 1 ) .
Solution using similar triangles:
Since vertical angles are congruent and A B ∥ C D ⟹ alternate interior angles are congruent ⟹ △ A B P ∼ △ D P Q ⟹
1 a = a − x x ⟹ x = a + 1 a 2 ⟹ A △ A B P = 2 ( a + 1 ) a 3 = 2 a
⟹ a ( a 2 − a − 1 ) = 0 a > 0 ⟹ a = 2 1 + 5 = ϕ and P : ( 1 , ϕ − 1 ) .
(Ignore the 1 in the diagram above. I have no idea how it got there.)
Using the above information and the diagram above ⟹ P P 1 = P P 2 = ϕ − 1 and P P 3 = P P 4 = 1
⟹ the slant heights s 1 = s 2 = ϕ 2 + ( ϕ − 1 ) 2 = 4 ( 1 + 5 ) 2 + 4 ( 5 − 1 ) 2 = 3
and
s 3 = s 4 = 1 + ϕ 2 = 1 + 4 ( 1 + 5 ) 2 = 4 1 0 + 2 5 = 2 5 + 5 = 5 ϕ
⟹ the lateral surface area S = ϕ ( 5 ϕ + 3 )
and the height P R = A B = ϕ ⟹ P R S = 5 ϕ + 3 = α ϕ + β
⟹ α + β = 8 .