OCR A Level: Decision 1 - Simplex [June 2012 Q4]
Consider the following linear programming problem.
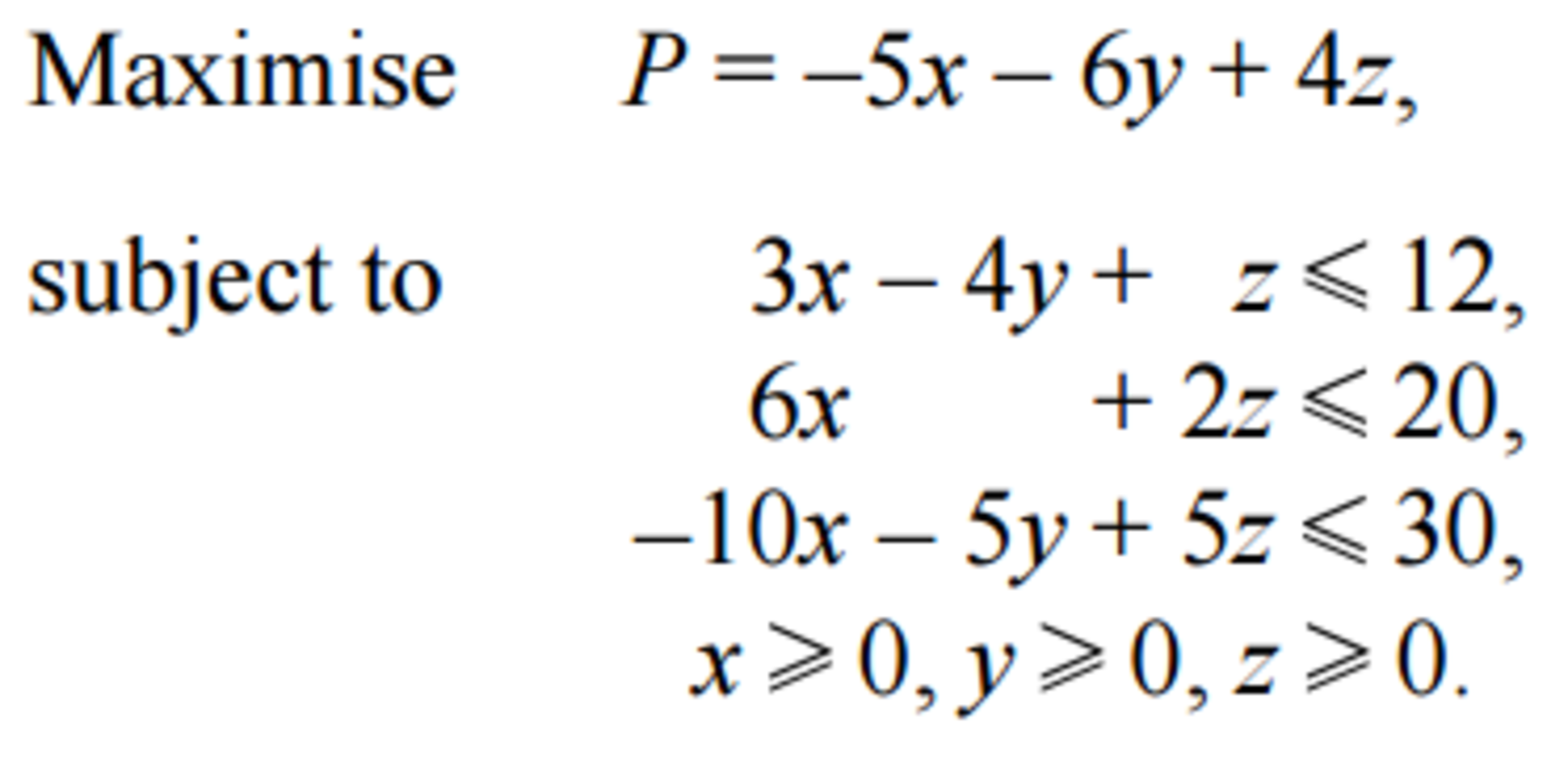 Use slack variables
,
and
to rewrite the first three constraints as equations. What restictions are there on the slack variables?
Use slack variables
,
and
to rewrite the first three constraints as equations. What restictions are there on the slack variables?
Represent the problem as an initial Simplex tableau.
Show why the pivot for the first iteration of the Simplex algorithm must be the coefficient of in the third constraint.
Perform one iteration of the Simplex algorithm, showing how the elements of the pivot row were calculated and how this was used to calculate the other rows.
Perform a second iteration of the Simplex algorithm and record the values of , , and at the end of this iteration.
Write down the values of , and from your final tableau and explain what they mean in terms of the original constraints.
Input as your answer.
There are 2 marks available for part (i), 2 marks for part (ii), 2 marks for part (iii), 3 marks for part (iv), 3 marks for part (v) and 2 marks for part (vi).
In total, this question is worth 19.4% of all available marks in the paper.
This is part of the set OCR A Level Problems .
The answer is 264.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The mark scheme for this question:
 Large Version (Page 1)
Large Version (Page 1)
Large Version (Page 2)