OCR A Level: Further Pure 2 - Rectangle Approximation [January 2010 Q7]

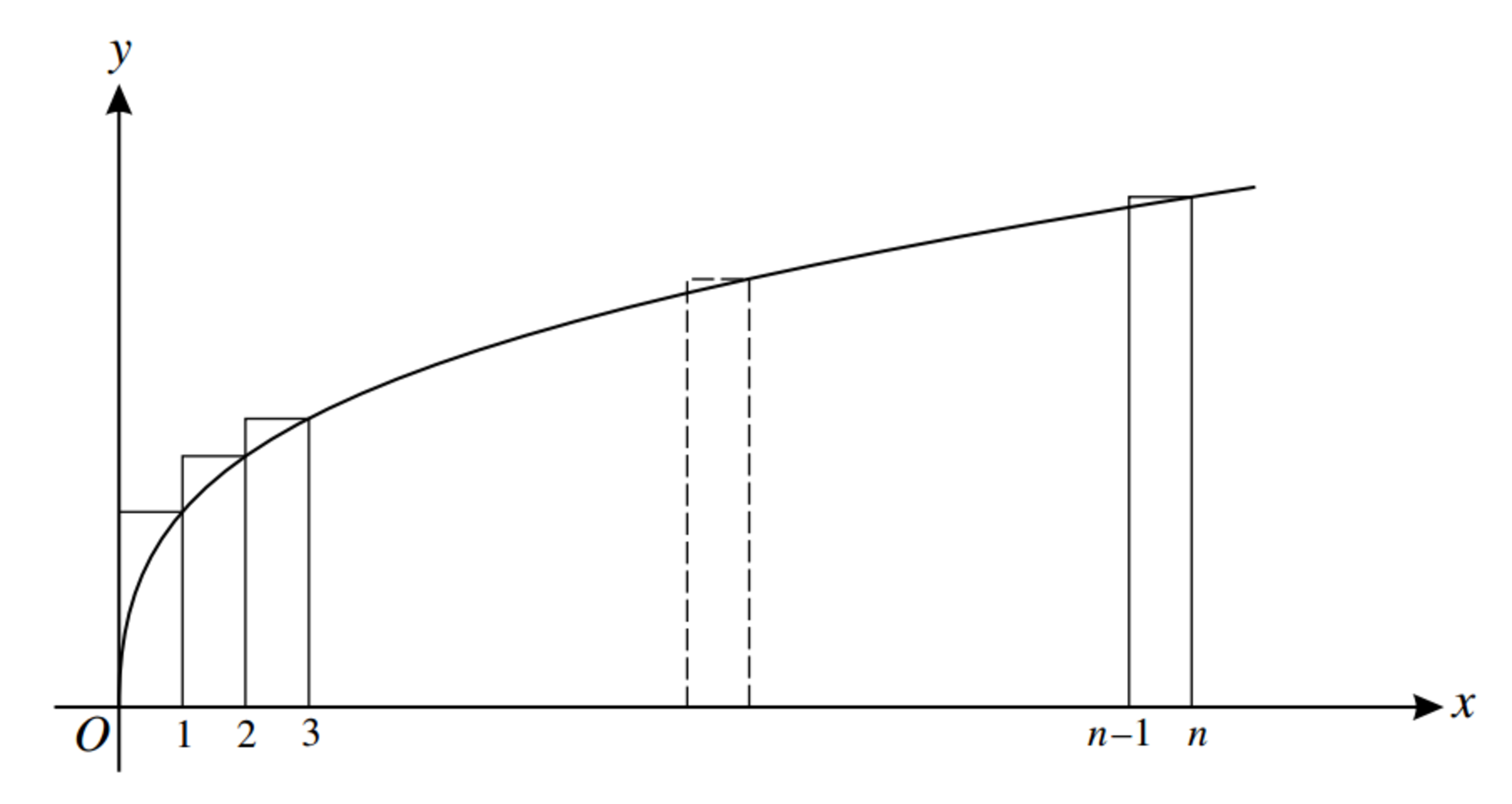The diagram shows the curve $y=\sqrt [ 3 ]{ x }$ , together with a set of $n$ rectangles of unit width.

$(\text{i})$ By considering the areas of these rectangles, explain why $\sqrt [ 3 ]{ 1 }+\sqrt [ 3 ]{ 2 }+\sqrt [ 3 ]{ 3 }+\cdots+\sqrt [ 3 ]{ n } > \int _{ 0 }^{ n }{ \sqrt [ 3 ]{ x } } \, dx .$ $(\text{ii})$ By drawing another set of rectangles and considering their areas, show that $\sqrt [ 3 ]{ 1 }+\sqrt [ 3 ]{ 2 }+\sqrt [ 3 ]{ 3 }+\cdots+\sqrt [ 3 ]{ n } < \int _{ 1 }^{ n+1 }{ \sqrt [ 3 ]{ x } } \, dx .$ $(\text{iii})$ Hence find an approximation to $\displaystyle \sum _{ n=1 }^{ 100 }{ \sqrt [ 3 ]{ n } }$ , giving your answer correct to 2 significant figures .

---

Input your answer to part $(\text{iii})$ .

---

There are 2 marks available for part (i), 3 marks for part (ii) and 3 marks for part (iii).

In total, this question is worth 11.1% of all available marks in the paper.

---

This is part of the set OCR A Level Problems .