OCR A Level: Further Pure 3 - Differential Equations [January 2010 Q6]
The variables and satisfy the differential equation Find the complementary function of the differential equation.
Given that there is a particular integral of the form , where is a constant, find the general solution of the equation.
Find the solution of the equation for which and when .
Input the value of as your answer.
There are 2 marks available for part (i), 6 marks for part (ii) and 4 marks for part (iii).
In total, this question is worth 16.7% of all available marks in the paper.
This is part of the set OCR A Level Problems .
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The mark scheme for this question: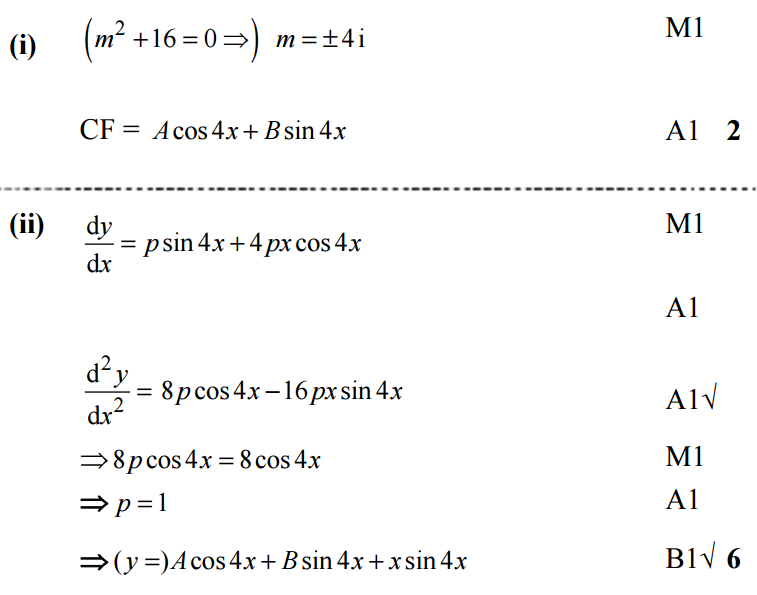
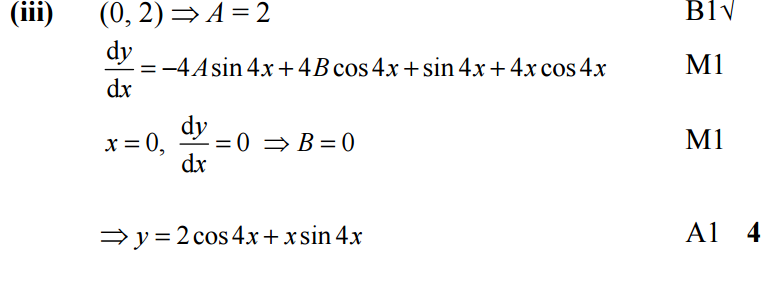 Large Version (Page 1)
Large Version (Page 1)
Large Version (Page 2)