OCR A Level: Mechanics 2 - Circular Motion [June 2010 Q5]
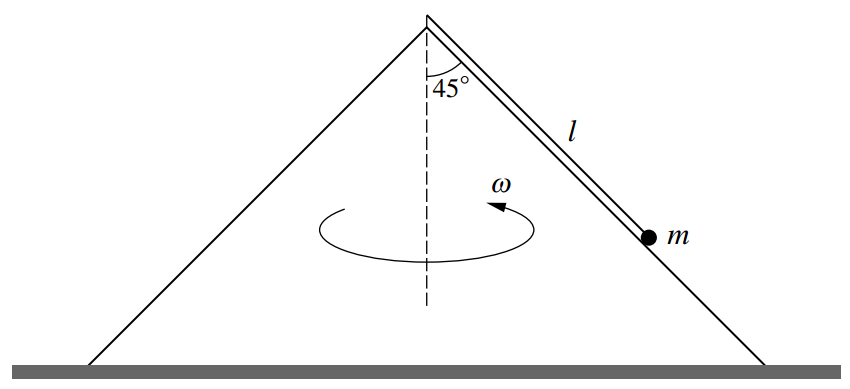 One end of a light inextensible string of length l is attached to the vertex of a smooth cone of semivertical angle
. The cone is fixed to the ground with its axis vertical. The other end of the string is attached to a particle of mass
which rotates in a horizontal circle in contact with the outer surface of the cone. The angular speed of the particle is
(see diagram). The tension in the string is
and the contact force between the cone and the particle is
.
One end of a light inextensible string of length l is attached to the vertex of a smooth cone of semivertical angle
. The cone is fixed to the ground with its axis vertical. The other end of the string is attached to a particle of mass
which rotates in a horizontal circle in contact with the outer surface of the cone. The angular speed of the particle is
(see diagram). The tension in the string is
and the contact force between the cone and the particle is
.
By resolving horizontally and vertically, find two equations involving and and hence show that .
When the string has length , calculate the greatest value of for which the particle remains in contact with the cone, to 3 significant figures.
Input your answer to part .
There are 6 marks available for part (i) and 4 marks for part (ii).
In total, this question is worth 13.9% of all available marks in the paper.
This is part of the set OCR A Level Problems .
The answer is 416.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Resolving the forces into horizontal and vertical components:
∣ ∣ T ∣ sin 4 π − ∣ R ∣ sin 4 π = R m v 2 = l sin 4 π m v 2 ∣ T ∣ sin 4 π + ∣ R ∣ sin 4 π = m g
Adding the two equations together:
2 ∣ T ∣ sin 4 p i = l sin 4 π m v 2 + m g = m ( l sin 4 π ) ω 2 + m g ⇒ ∣ T ∣ = 2 1 m ( l ω 2 + sin 4 π g ) = 2 1 m ( l ω 2 + 2 g )
Now, to find maximum o m e g a for which the ball stays in contact with the surface, we set R = 0 and use one of the expressions for tension:
∣ T ∣ sin 4 π + ∣ R ∣ sin 4 π = m g ⇒ ( sin 4 π ) 2 1 m ( l ω 2 + 2 g ) = m g ⇒ 2 1 ( 2 l ω 2 + g ) = g ⇒ 2 l ω 2 = g ⇒ ω m a x = l 2 g
ω m a x = l 2 g = 0 . 8 2 ( 9 . 8 1 ) = 4 . 1 6 rad / s