OCR A Level: Mechanics 2 - Sliding And Toppling [June 2011 Q7]
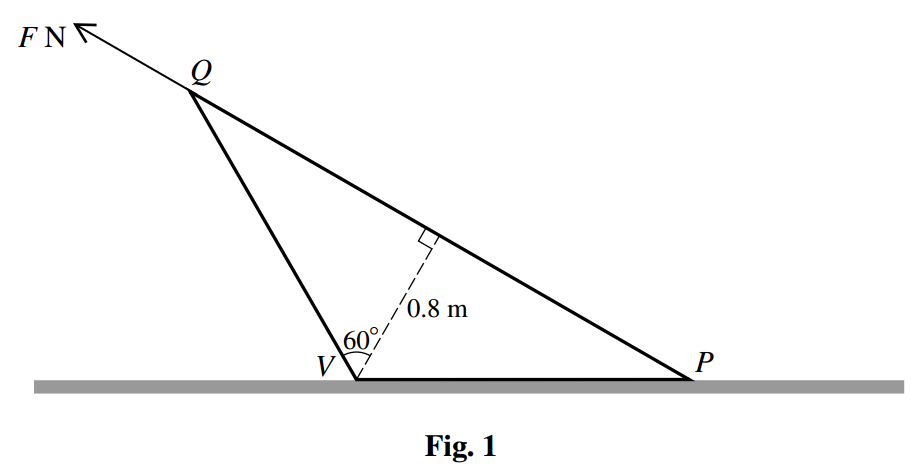
A uniform solid cone of height and semi-vertical angle lies with its curved surface on a horizontal plane. The point on the circumference of the base is in contact with the plane. is the vertex of the cone and is a diameter of its base. The weight of the cone is . A force of magnitude and line of action is applied to the base of the cone (see Fig. 1). The cone topples about without sliding.
Calculate the least possible value of .
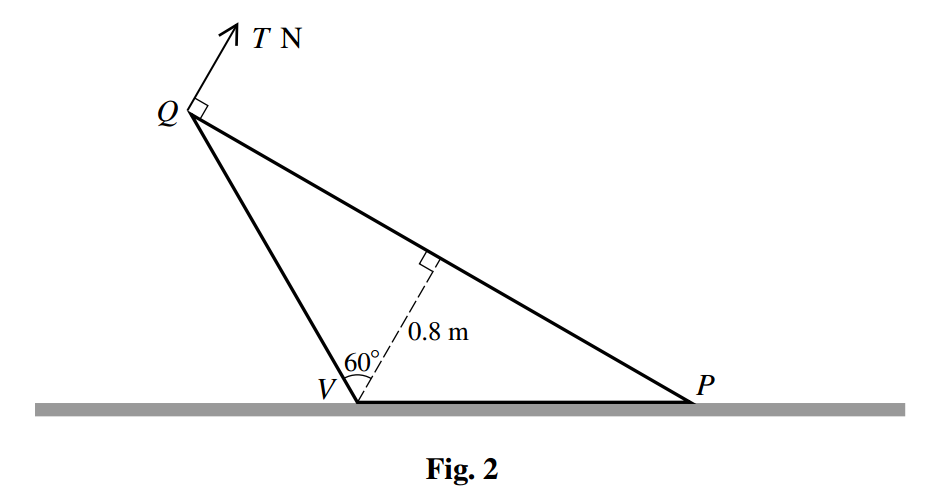 The force of magnitude
is removed and an increasing force of magnitude
acting upwards in the vertical plane of symmetry of the cone and perpendicular to
is applied to the cone at
(see Fig. 2). The coefficient of friction between the cone and the horizontal plane is
.
The force of magnitude
is removed and an increasing force of magnitude
acting upwards in the vertical plane of symmetry of the cone and perpendicular to
is applied to the cone at
(see Fig. 2). The coefficient of friction between the cone and the horizontal plane is
.
Given that the cone slides before it topples about , calculate the greatest possible value for .
Input the nearest integer to as your answer.
There are 4 marks available for part (i) and 10 marks for part (ii).
In total, this question is worth 19.4% of all available marks in the paper.
This is part of the set OCR A Level Problems .
The answer is 395.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The mark scheme for this question: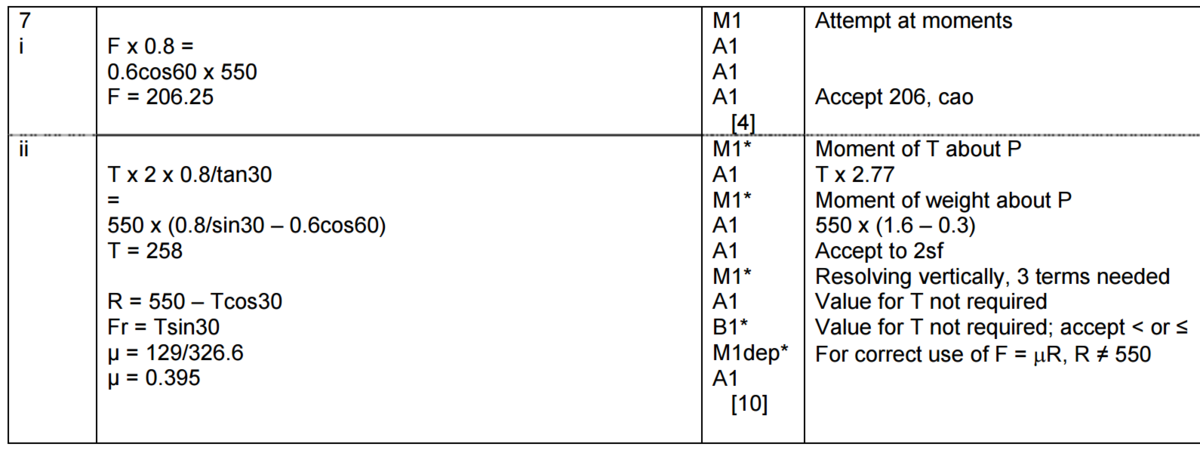 Large Version
Large Version