Octagon circumscribing a circle
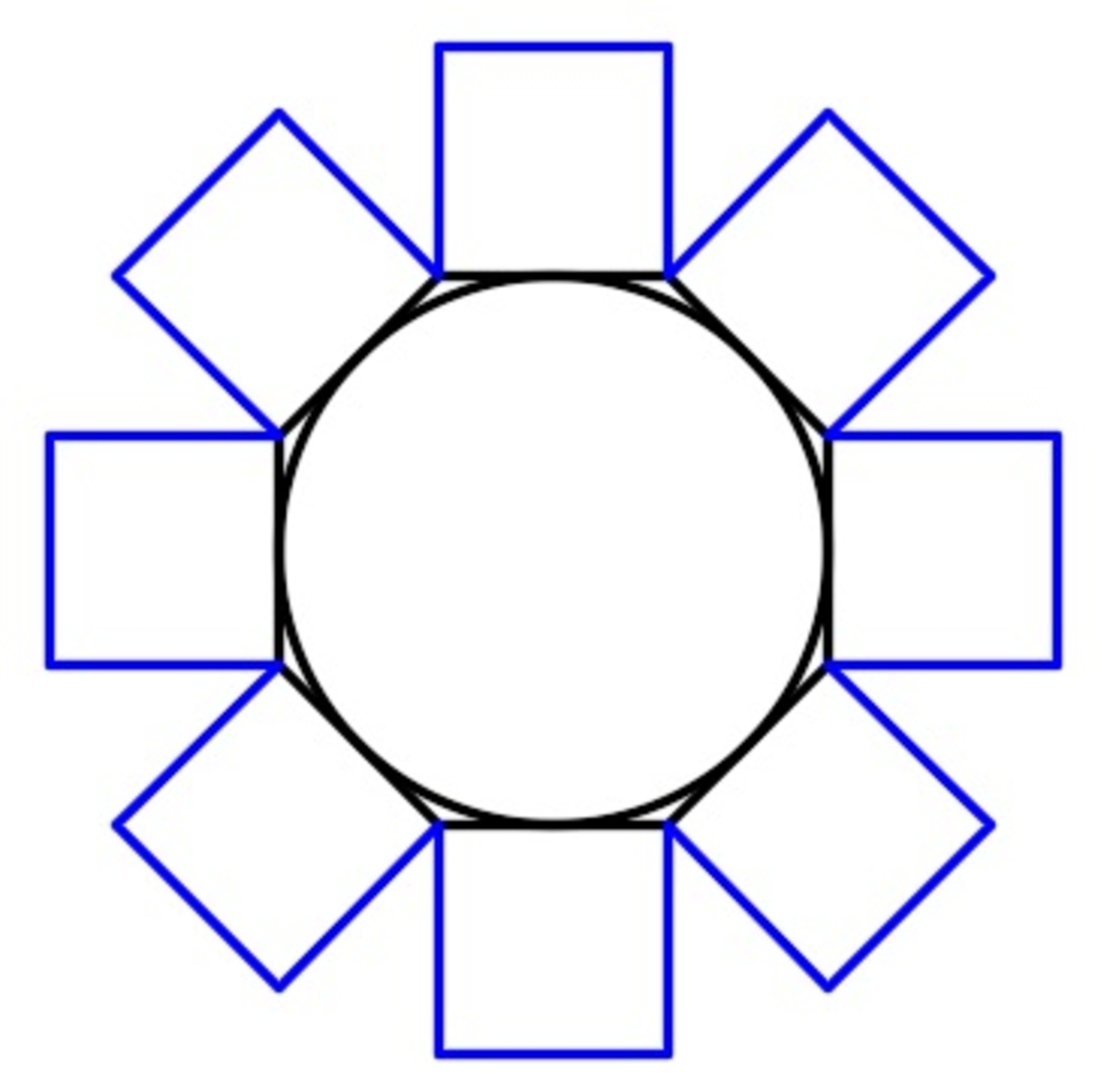 A circle is inscribed in a regular octagon as shown. Squares are drawn on each side of the octagon making each side of the octagon as one side of each square. If the perimeter of the figure (consider the blue color) is 96 units, find the area of the circle in square units. Round off your answer to the nearest integer.
A circle is inscribed in a regular octagon as shown. Squares are drawn on each side of the octagon making each side of the octagon as one side of each square. If the perimeter of the figure (consider the blue color) is 96 units, find the area of the circle in square units. Round off your answer to the nearest integer.
The answer is 73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The side length of the octagon is l = 2 4 9 6 = 4 . There are many ways to find the radius of the inscribed circle, the direct formula uses trigonometry, but there is another way. First we find the radius of the circumscribed circle, then we find the radius of the inscribed circle (the length of the apothem).
The radius R of the circumscribed circle in an octagon can be found as following:
l = R 2 − 2
4 = R 2 − 2
R = 2 − 2 4
The length of the inscribed circle radius r can be found as following:
r = 2 R 2 + 2
r = 2 2 − 2 4 2 + 2
r = 2 2 − 2 4 2 + 2
r = 2 2 − 2 2 − 2 4 2 + 2 2 − 2
r = 2 ( 2 − 2 ) 4 4 − 2
r = 2 − 2 2 2
Then the area of the inscribed circle will be:
( 2 − 2 2 2 ) 2 ⋅ π ≈ 7 3