Octagon inside a octagon
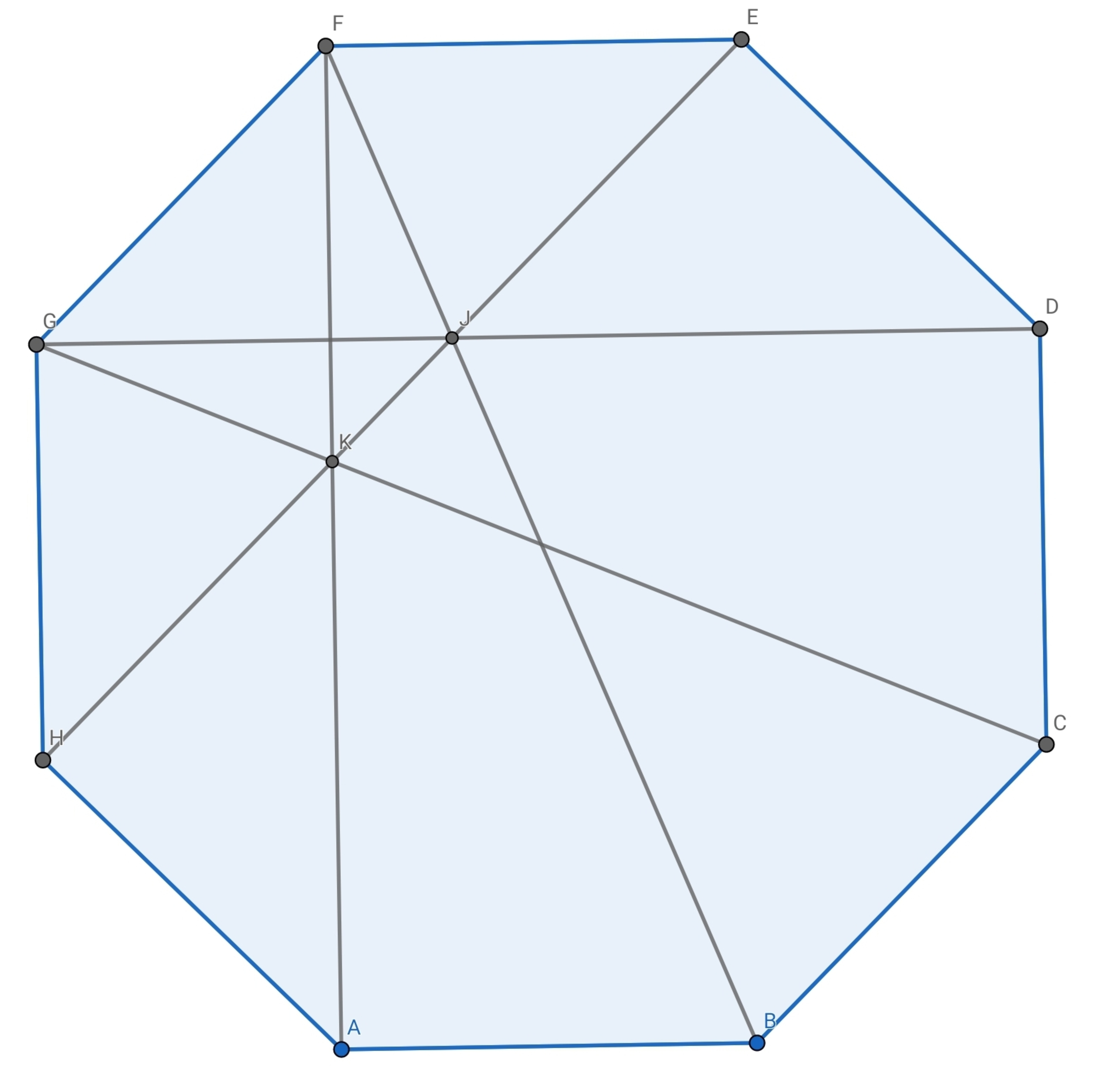
In the image there is regular octagon, the value of G F K J can be represented as a − b , where a and b are positive integers with a square-free. Find a + b .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thank you for posting
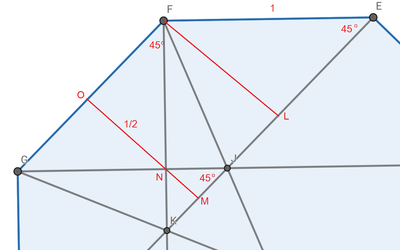
Let the side length of the regular octagon be 1 , G J and F K intersect at N , F L and O M , which passes through N , be perpendicular to H E . Note that △ E F L is an isosceles right triangle. Hence F L = O M = 2 1 . △ F N O is also an isosceles right triangle. This means that O F = O N = 2 1 . △ F G N and △ K J N are also isosceles right triangles and are hence similar. Then
G F K J = O N M N = O N O M − O N = 2 1 2 1 − 2 1 = 2 − 1
Therefore a + b = 2 + 1 = 3 .
Thank you for posting sir
Let the regular octagon be of unit side length. F E J G is a rhombus, thus, G J = F E = 1 .
Consequently, H G J is an isosceles right triangle, hence, by Pythagorean theorem,
H J = H G 2 + G J 2 = 1 2 + 1 2 = 2 G F K H is also a rhombus, thus, H K = G F = 1 .
Hence, the ratio in question is G F K J = G F H J − H K = 1 2 − 1 = 2 − 1 For the answer, a = 2 , b = 1 , thus, a + b = 3 .