Octagonal Resistor System

Let current $I$ enters at the terminal $A$ , the same amount of current must exit at the terminal $B$ . The circuit is symmetric about the perpendicular bisector of the line $AB$ , thus, rest of the current can be distributed as shown in the diagram (the circuit in left).

The current is distributed in such a way that the junction at the center of the octagon can be broken as shown in the diagram (the circuit in right) without affecting the distribution of the current.

The final circuit can be easily solved by repetitively applying the series and parallel combinations to get $R_{\text{eff}} = \frac{58}{105} \times 420 = 232 \Omega$ .

I'm sure that someone will post a clever solution, but this is also a nice problem for practicing forming the "Y Bus" or "Nodal Admittance Matrix" for a system. Label the node voltages $V1$ through $V7$ as shown in the (equally shabby) picture. For simplicity, assume that we have a $1V$ source connected between $A$ and $B$ , and that each resistor has a value of $1 \Omega$ . We will multiply by 420 at the end.

Nodal Admittance Matrix Formation Rules (Note: "Admittance" refers to the reciprocal of resistance):

1) Populate the diagonal terms with the sum of the admittances connected to each corresponding node.
2) Populate the off-diagonal terms with the negative of the admittance between the two corresponding nodes.

The rule for populating the vector on the other side is:

If the node is connected to a node with a known voltage, populate the corresponding entry in the vector with the known voltage multiplied by the admittance between the node and the known voltage.

This is all just a quick and convenient shorthand for the traditional nodal analysis. Using these rules, we can easily form the system shown below.

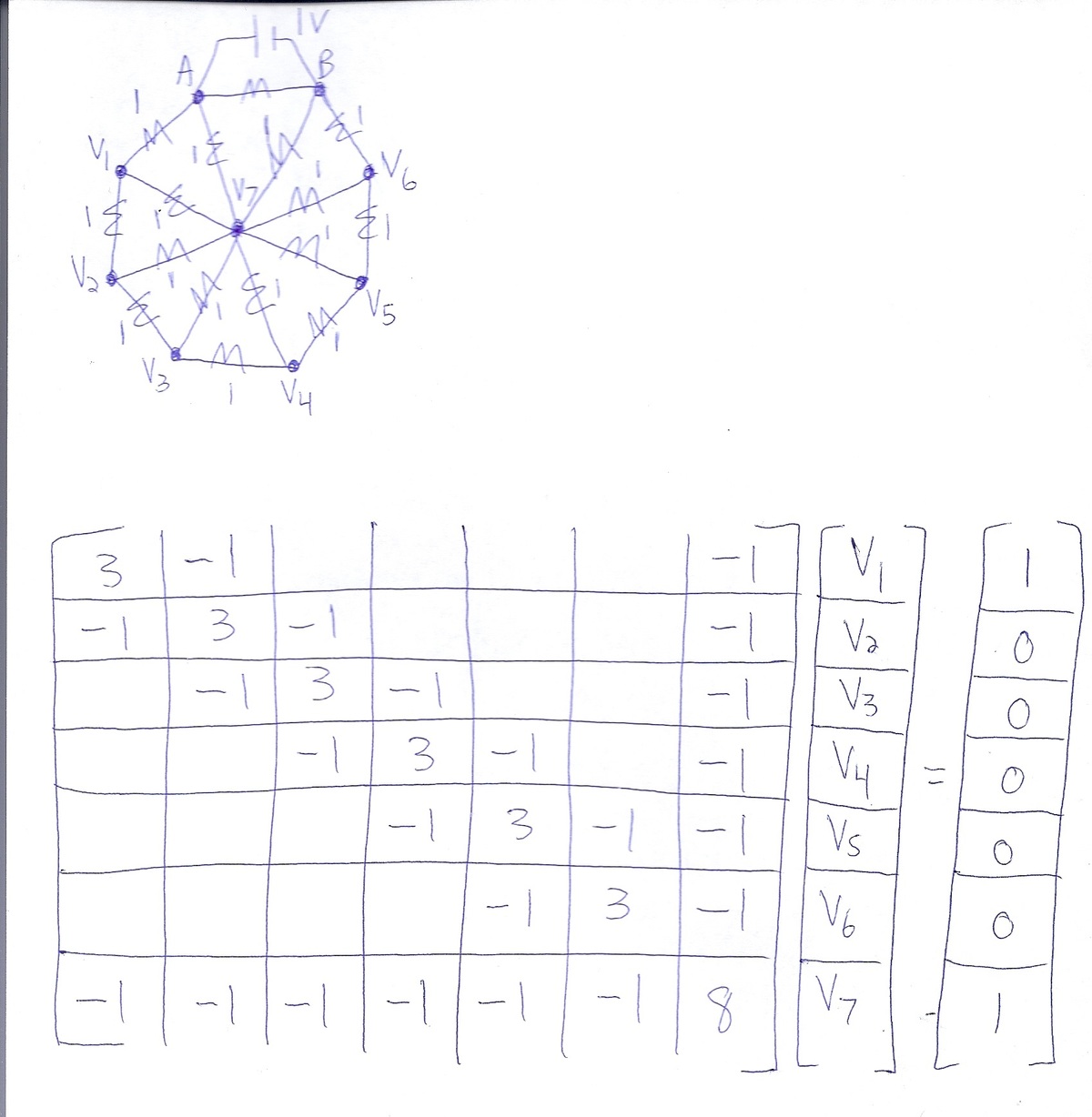
Inverting and pre-multiplying gives (we only need $V1$ and $V7$ ):

$V1 = 0.689655172, V7 = 0.5$

The current from the source is:

$\large{I_{src} = \frac{1-V_1}{1} + \frac{1-V_7}{1} + \frac{1-0}{1} \approx 1.810344828}$

The equivalent resistance is:

$\large{R_{eq} = \frac{1}{I_{src}} \approx 0.552380952 \\ 420 * R_{eq} \approx \boxed{232}}$

Assume all resistors as $R$ .

A regular octagon has a vertical line of symmetry so we just apply Vertical Symmetry to the resistor system.

Then applying parallel and series combinations repetitively, we get final answer as $\frac{58}{105}$ $R$ . Now we just have to substitute $R$ $=$ $420$ $ohms$ . Thus $R_{eq}$ = $\frac{58}{105}$ $*$ $420$ $=$ $232$ $Ohms$

Symmetry is a very good concept for solving complex circuits.You can understand it better here .

Question is original and made by me (with some inspiration from a $hexagon$ system from INJSO 2015).Hope you liked it.