Octagonal Rose
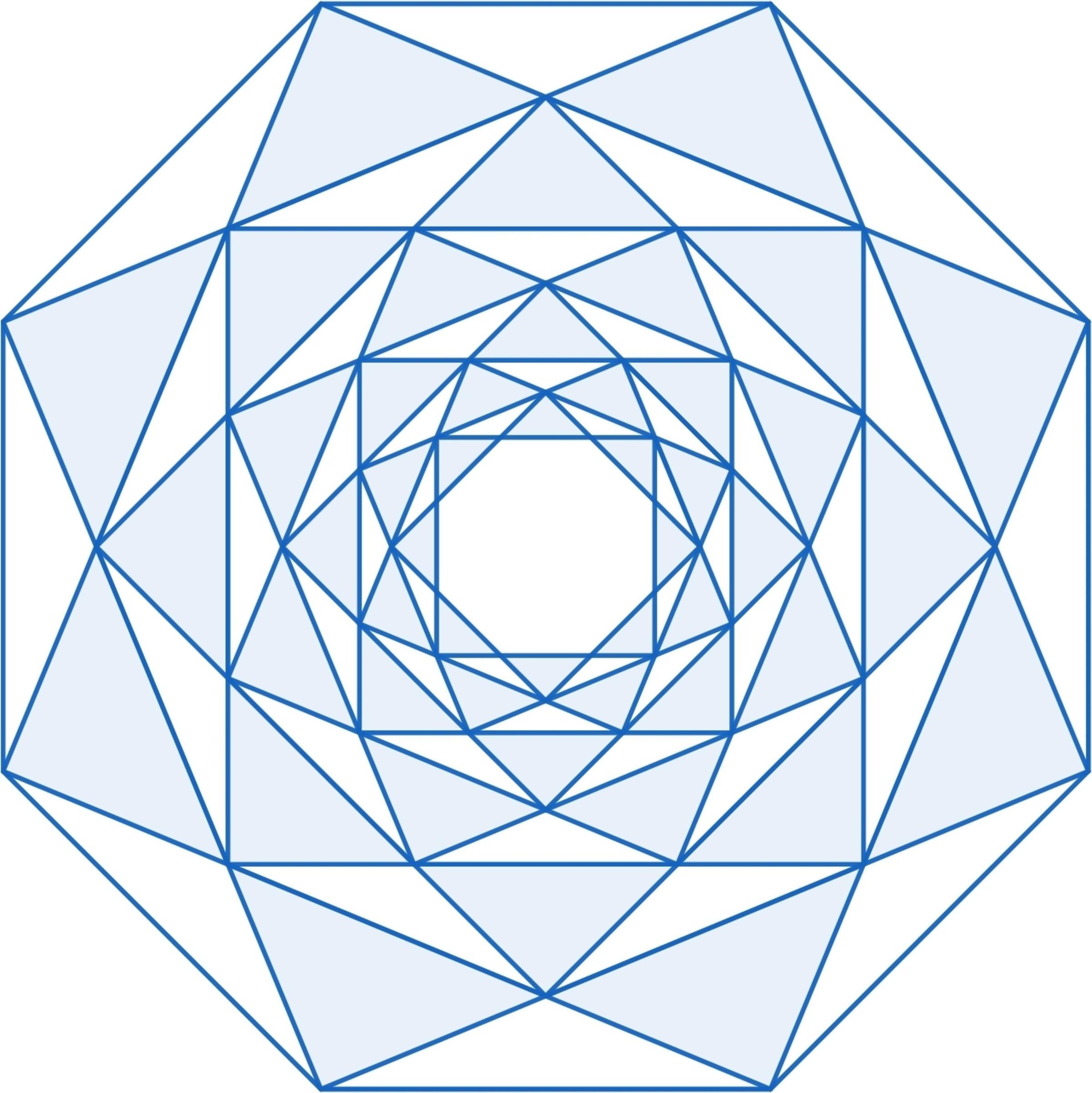
The outermost rectangular octagon is of side length 1. The pattern in the above figure goes till infinity. Now the total area of the shaded region can be represented as where is a natural number . Find
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The entire octagonal rose can be tiled by different sizes of the following tile, all with the same ratio of shaded to unshaded parts, where x = A D = D B = B C and ∠ A D B = 9 0 ° :
The area of △ A D B is A △ A D B = 2 1 ⋅ x ⋅ x = 2 1 x 2 and the area of △ D B C is A △ D B C = 2 1 ⋅ x ⋅ x sin 1 3 5 ° = 4 2 x 2 , so the ratio of shaded to the whole is A △ A D B + A △ D B C A △ A D B = 2 1 x 2 + 4 2 x 2 2 1 x 2 = 2 − 2 .
This ratio is maintained for the whole regular octagon, which has an area of A oct = 2 ( 1 + 2 ) , so the area of the shaded region is ( 2 − 2 ) A oct = ( 2 − 2 ) ⋅ 2 ( 1 + 2 ) = 8 , which makes a = 8 .