Octarelate
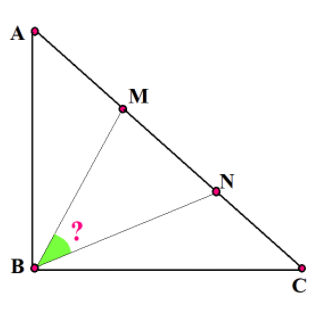
The figure shows a right triangle with the right angle at .
and are 2 points on such that .
Find the measure of the angle in degrees.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Triangle A B C and three others identical to it are pictured in red are organized to form a square as shown.
The original image made the triangle appear to be isosceles, but the problem did not state that it was and it does not need to be. So I make it a general right triangle.
The condition that A M 2 + N C 2 = M N 2 translates, thanks to the Pythagorean theorem, into M N = N M ’ where M ′ is a point equivalent to M in the next triangle.
This means that the black octagon has sides of equal lengths.
It is inscribed into a square, so it could be tempting to assume that it is a regular octagon and that the angle
∠ M O N = 8 3 6 0 ∘ = 4 5 ∘
...
However, the octagon need not be regular, as shown in the lower image.
The triangles O N M and O N M ’ are no longer isosceles, but they are still congruent.
All of their sides are the same size, since the side O N is shared, M N = N M ’ and O M = O M ’ .
Therefore the angles ∠ M O N and ∠ N O M ’ are equal to each other.
They are also equal to the remaining 6 such angles.
So we can conclude that even in the general case
∠ M O N = 8 3 6 0 ∘ = 4 5 ∘