Odd Circles
A family of infinite circles, all share a common tangent. All gray circles are tangent to white circle, and to two neighbour gray circles.
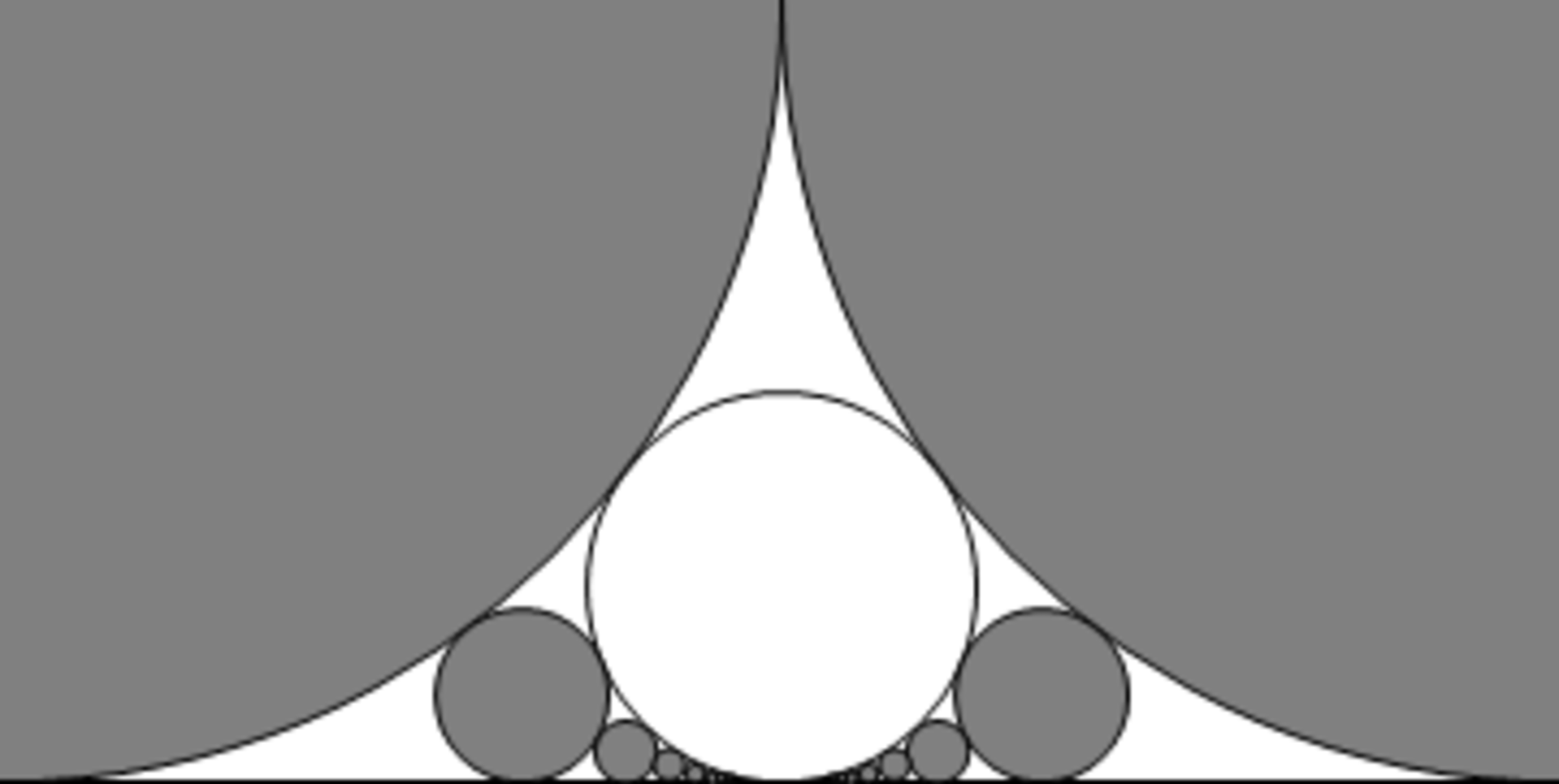 The 2 largest gray circles are unit circles (both not fully shown), the total area of gray circles can be expressed as
B
A
π
C
, where
A
,
B
,
C
are integers and
A
,
B
share no common factor. Find the value of
1
0
0
0
0
A
+
1
0
0
B
+
C
.
The 2 largest gray circles are unit circles (both not fully shown), the total area of gray circles can be expressed as
B
A
π
C
, where
A
,
B
,
C
are integers and
A
,
B
share no common factor. Find the value of
1
0
0
0
0
A
+
1
0
0
B
+
C
.
Hint: ζ
The answer is 14805.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
We can use Descarte's Theorem to find the radii of four mutually tangent circles.
k 4 = k 1 + k 2 + k 3 − 2 k 1 k 2 + k 2 k 3 + k 3 k 1
where k 1 , k 2 , k 3 , k 4 = r 1 1 , r 2 1 , r 3 1 , r 4 1
If k 1 , k 2 , k 3 = 0 , 1 , 1 , then r 4 = 4 1 , which is the radius of the white circle.
Then if k 1 , k 2 , k 3 = 0 , 4 , k i , then k i + 1 = ( 2 + k i ) 2
This means that the radii of the gray circles are 1 , 3 2 1 , 5 2 1 , 7 2 1 , . . . , so that the total area is (with help from the hint)
r = 1 ∑ ∞ ( 2 r − 1 ) 4 2 π = 4 8 π 5
so that the answer is 1 4 8 0 5
Note:
r
=
1
∑
∞
(
2
r
−
1
)
4
1
=
(
1
−
2
4
1
)
ζ
(
4
)
=
9
6
π
4
nice and concise solution, though i think the sigma sum should start with r=1
Log in to reply
uh, fixed, yeah, the expression started out with 2 r + 1 , so missed that detail.
Study the visual proof above, hence prove that three mutually tangent circle sharing a common tangent, their radii are related by r 1 1 + r 2 1 = r 3 1
By using the formula, proof that the radius of white circle is 4 1 , the radii of gray circles are 1 , 3 2 1 , 5 2 1 , 7 2 1 , 9 2 1 , . . . 2b. (Optional) Use mathematical induction to prove the radius of k-th gray circle is ( 2 k − 1 ) 2 1 .
By using the definition of Riemann zeta function, show that 1 + 3 4 1 + 5 4 1 + 7 4 1 + 9 4 1 + . . . = ( 1 − 2 4 1 ) ζ ( 4 )
Given ζ ( 4 ) = 9 0 π 4 , show that the total area of gray circles is 2 ⋅ π ⋅ 1 6 1 5 ⋅ ζ ( 4 ) = 4 8 1 π 5
∴ A = 1 , B = 4 8 , C = 5 , 1 0 0 0 0 A + 1 0 0 B + C = 1 4 8 0 5