Oddly Divisible 2

let the number be $x$ :

$(1,2,3,4,6,7,8,9) | x \Rightarrow 7 \times 8 \times 9 | x \Rightarrow 504 | x$

Obviously 504 is not palindrome, so $x \geq 2 \times 504 > 1000$ , i.e. $x$ has at least 4 digits.

if $x$ has 4 digits:

let $x = \overline {abba} = 1001 \cdot a + 110 \cdot b = 7 \times 143 \cdot a + 2 \times 5 \times 11 \cdot b$

$9 | x \Rightarrow 9 | (a+b+b+a) \Rightarrow 9 | (a+b)$

$7 | x \Rightarrow 7 | \overline {abba} \Rightarrow 7 | b$

$\therefore b = 7, a = 2, x = 2772$

but $8 \nmid 2772$ , so $x$ must have more than 4 digits.

if $x$ has 5 digits:

let $x = \overline {abcba} = 8 \times 125 \cdot \overline {ab} + \overline {cba}$

$8 | x \Rightarrow 8 | \overline {cba}$

Then $\overline {cba}$ must be one of (c is even):

• c08

• c16

• c24

• c32

• c48

• c56

• c64

• c72

• c88

• c96

or (c is odd):

• c04

• c12

• c28

• c36

• c44

• c52

• c68

• c76

• c84

• c92

As $9 | x$ , it is easy to get c ( $c = 9k - 2a - 2b$ ). And $7 | x$ , then we can get the solution $x = 48384$

Q.E.D.

Since the palindrome number is divisible by $1$ , $2$ , $3$ , $4$ , $6$ , $7$ , $8$ , and $9$ , it must be divisible by the lowest common multiple $\text{lcm }(1,2,3,4,6,7,8,9) = 7 \times 8 \times 9 = 504$ . Therefore the palindrome number must be a multiple of $504$ . Using Python coding the smallest of such multiple is $\boxed{48384}$ .

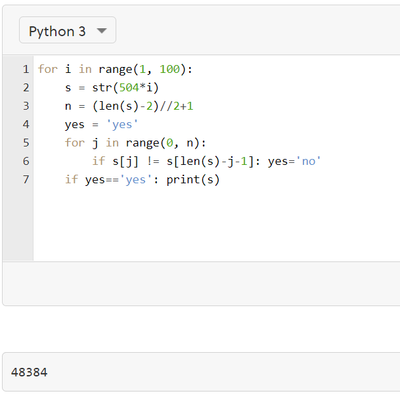
What the meaning of " is divisible to all digits except for $5$ and $0$ "?

I suppose the author wanted to say "is divisible by all 1 digit numbers except $5$ . Divisibility by $0$ is not determinable.