Oddly Enough
Two real numbers a and b are randomly chosen from the range ( 0 , 1 ) . The probability that b a rounded to the nearest integer is odd is equal to P . What is ⌊ 1 0 0 0 P ⌋ ?
The answer is 535.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Really well written solution Jatin :)
NICE!!!!!!
One can use Monte Carlo method with computer with this code:
1 2 3 4 5 6 7 8 9 10 11 |
|
I did the same thing. The best thing for solving probability problems really just seems to be to test it ten million times and see what happens.
Python:
1 2 3 4 5 6 7 8 9 10 |
|
Log in to reply
I always like to simulate probability problems first as well, but ... convergence is usually very slow, and in the end, it's not exact.
What about floor(100000000000000*P)?
Although Monte-Carlo would have been easy I decided against it after I made this diagram, on the grounds that such results might be subject to considerable variation. On the other hand, I have a congenital disinclination for reducing infinite series.
I decided to proceed by summing areas. Since the region corresponding to the first odd integer is miserable to work with I decided to sum the even-numbered regions instead. The boundaries of these are obviously equations like y=x/1.5 and y=x/2.5, y=x/3.5 and y=x/4.5, and so on. The probability of the region where x/y rounds to 0 is 0.25. To avoid round-off errors I made the summation using fractions.
1 2 3 4 5 6 7 8 9 10 11 12 13 |
|
Convergence was slow (reminding me of one of Euler's calculatiosn). The final value here was 0.214576334205 giving a probability of 1-(.25+0.214576334205) or 0.535423665795.
Consider the problem geometrically. We have points ( a , b ) confined within a unit square with its bottom left vertex at the origin.
Let [ b a ] be b a rounded to the nearest integer.
We have
[ b a ] = 1 ⟺ 2 1 ≤ b a < 2 3 ⟺ b ≤ 2 a < 3 b
[ b a ] = 3 ⟺ 2 5 ≤ b a < 2 7 ⟺ 5 b ≤ 2 a < 7 b
And so on. We can interpret these regions in the following diagram.
https://www.desmos.com/calculator/p1nf8wndrs
Where the shaded regions are those where [ b a ] is odd.
To avoid dealing with the larger, non-triangular region differently, just subtract the non-shaded area from 1.
Pr ( [ b a ] is even ) = 2 1 ⋅ 1 ⋅ ( 2 1 + ( 3 2 − 5 2 ) + ( 7 2 − 9 2 ) + ( 1 1 2 − 1 3 2 ) + . . . ) = 4 1 + 3 1 − 5 1 + 7 1 − 9 1 + . . . = 4 1 + 1 − ( 1 − 3 1 + 5 1 − 7 1 + . . . ) = 4 5 − 4 π by the Leibniz formula for π = 4 5 − π
We then have that Pr ( [ b a ] is odd ) = 1 − 4 5 − π = 4 π − 1 .
⌊ 1 0 0 0 ⋅ 4 π − 1 ⌋ = 5 3 5
Extra Information
- To prove that 1 − 3 1 + 5 1 − 7 1 + . . . , we have that arctan θ = θ − 3 θ 3 + 5 θ 5 from its Maclaurin series. Substituting θ = 1 gives the result.
- A similar problem was covered by 3Blue1Brown, from where I learnt this method.
Wow, this was fun and kind of unexpected. What's interesting is that if the Floor of a/b was used instead of Round of a/b, we'd end up with (1/2)Log(2) instead of something involving π. How about that?
It would have been simpler if that was floor of a/b. Infact, at once, I interpreted it as floor of a/b and got answer as 2 1 ln 2 . Also, this was really unexpected, as it never seems to be a calculus problem in first look.
Log in to reply
That's exactly what happened to me, I have a bad habit of trying to solve problems before I fully understand the question, and I came up with the answer (1/2)Log(2) first. Now that π has entered into the picture, I'm really fascinated with this problem. A "must remember" problem.
This is best suited for a comment, not a solution. But that's a good problem. If you want to submit it yourself, go ahead.
Log in to reply
Oh, right, I see where I should have replied. But Yadav's method is more or less the way I did it, so if I can, I'd like to try finding another solution that illustrates why π is involved. I'll have to think on that first.
Log in to reply
Good luck with that! My intended solution is what Jatin did with the triangles in the square to get the series.
First we show that the value of S = r = 0 ∑ ∞ 2 r + 1 ( − 1 ) r is 4 π . I have two methods here for the proof:
Method-1:
Clearly S = r = 0 ∑ ∞ ( − 1 ) r ∫ 0 1 x 2 r d x
= ∫ 0 1 ( r = 0 ∑ ∞ ( − 1 ) r x 2 r ) d x
= ∫ 0 1 1 + x 2 1 d x = 4 π
Method-2:
By series expansion of ln ( 1 + i ) , we see that S is its imaginary part. Hence, S = Im ( ln ( 2 e i 4 π ) ) = Im ( ln ( 2 ) + i 4 π ) = 4 π
Now, let us come to the problem. Let me use y in place of a and x in place of b .
Clearly, as the integer nearest to x y is odd, hence,
x y ∈ ( 1 / 2 , 3 / 2 ) ∪ ( 5 / 2 , 7 / 2 ) ∪ ( 9 / 2 , 1 1 / 2 ) ∪ …
Now, as x , y ∈ ( 0 , 1 ) , area of sample space is 1 .
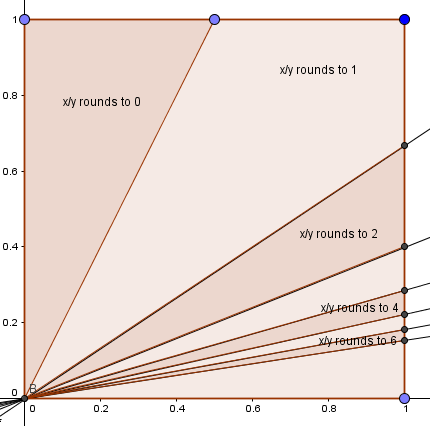
Given below is a graph, showing triangles 1 , 2 , 3 , 4 , 5 , …
Clearly, area of favorable region = Ar(1)+Ar(2)+Ar(4)+Ar(6)+Ar(8)+ …
Now, altitude of each of these triangles is 1
Hence, area of favorable region = 2 1 × 1 × ( 1 − 1 / 2 + 1 − 2 / 3 + 2 / 5 − 2 / 7 + 2 / 9 − 2 / 1 1 + 2 / 1 3 − 2 / 1 5 … )
= 2 1 ( 2 S − 2 1 )
= 4 π − 1 ≈ 0 . 5 3 5 4
This is the required probability as area of sample space is 1 . Hence, answer is 5 3 5