Oddly pointed
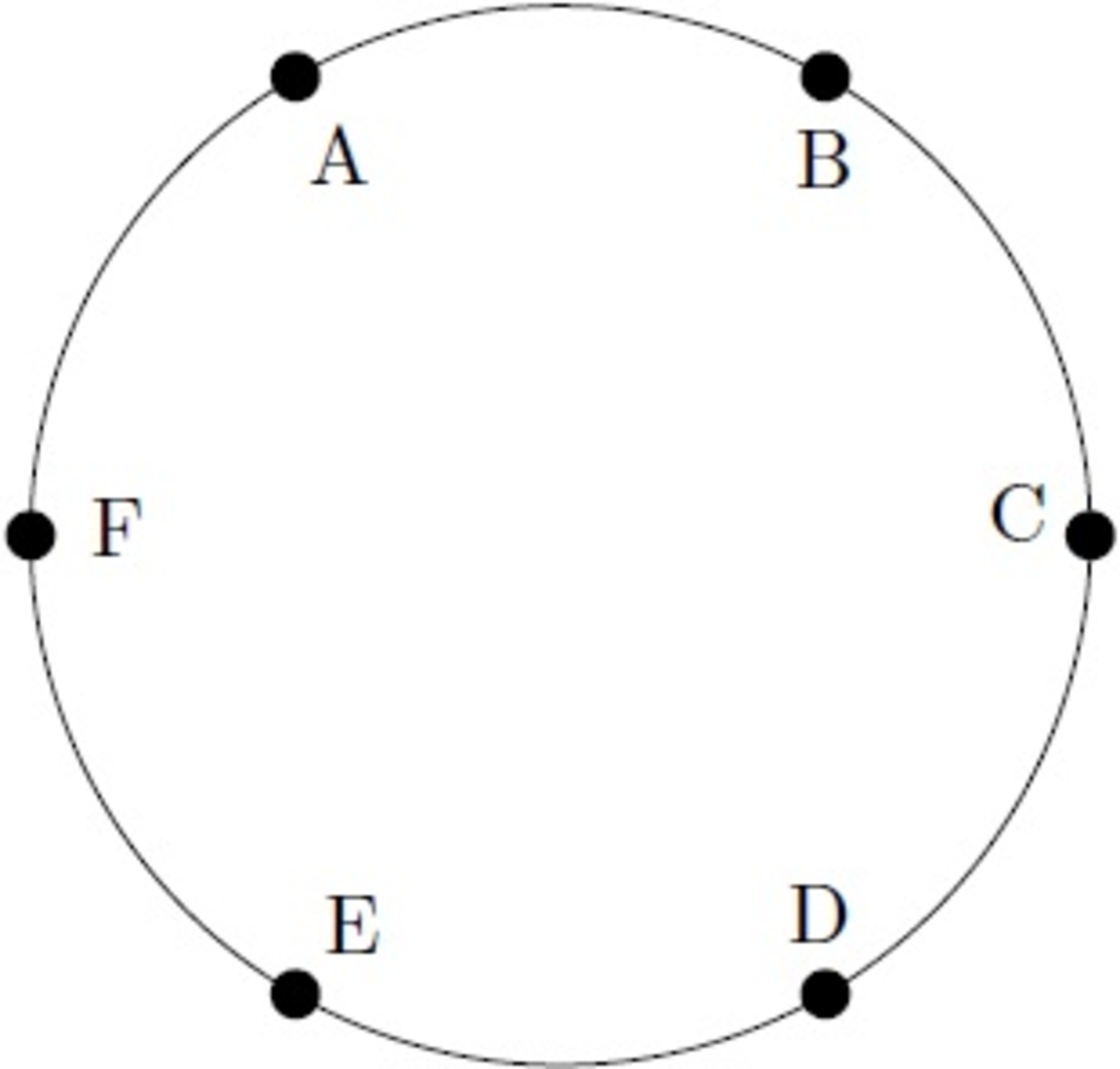
The numbers 1 , … , 6 are to be placed in some order at the points A , … , F in the figure below. How many ways can the numbers be placed so that each sum of consecutive pairs of points is odd?
The answer is 72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
3! * 3! * 2
don't you think 72 should be divided by 6 because of the rotational symmetry?
Log in to reply
No, as it is implied that the points are represented by letters, ABCDEF, and it's really finding possible values for these letters which are in the pattern of even-odd-even-odd-even-odd or odd-even-odd-even-odd-even, so in this case there is no rotational symmetry, as we are not going around the table but rather finding values for the points.
A simple trick is to look at the odd and even numbers
Let us start by placing 1 . We can place 1 at any of the 6 available places. That means we have 6 choices for placing 1 . Suppose that in a particular realization, we place 1 at point A . Now we must place even integer at point B since sum of A and B must be odd. Thus we have 3 choices for point B : 2 , 4 or 6 . Again for a given choice of B , we have remaining 2 choices for point F because even at F we must have even integer due to the odd sum constraint for A and F . After this, we should place odd integer at C because of same constraint. But for this, we have only 2 choices: 3 and 5 since we have already placed 1 at A . Now we have one even and one odd integer to place and they must be placed at D and E respectively.
Hence in total, we have 6 ( A ) ∗ 3 ( B ) ∗ 2 ( F ) ∗ 2 ( C ) ∗ 1 ( D ) ∗ 1 ( E ) = 7 2 ways to place integers as required.
First notice that for the sum of consecutive pairs to be odd, the pair has to include 1 odd and 1 even number. This means we will have the pattern, Odd Even Odd Even Odd Even .
Since we have 3 choices of each the number of permutations we can make is:
3 ⋅ 3 ⋅ 2 ⋅ 2 ⋅ 1 ⋅ 1 = 3 6
Now if position didn't matter that would be our answer. However, since each position is label then:
A 1 B 2 C 3 D 4 E 5 F 6 = B 1 C 2 D 3 E 4 F 5 A 6
Assume that in our original permutation our starting position was A , now if we change our starting position to B we should get an addition 36 possibilities. We can see this clearly by looking at the position of the Odd and Even numbers.
When our starting position is A , We have Odd numbers at points A , C , and E ; and Even numbers at points B , D , and F .
When our starting position is B , We have Odd numbers at points B , D , and F ; and Even numbers at points A , C , and E .
This means it is impossible for any of the possibilities from starting position A to overlap with possibilities from starting position B .
However, the same is not true when we choose C or any other point as our starting position since any possibilities we get from each of those starting points will overlap with either A or B .
So our final number of possibilities is:
3 6 ⋅ 2 = 7 2
If the sum of two numbers is odd then one of them is even and the other is odd.
Then either A is odd, B is even, C is odd and so on, or the opposite: A is even and so on.
Taking the first case:
A , C and E are odd.
The number of ways to order the odd numbers is 3 ! = 6 .
The same is true for the even numbers in positions B , D and F : 3 ! = 6 .
Now, the number of arrangements is the product of the ways to order the odd numbers and the even numbers, which is 6 × 6 = 3 6
We double this because of the cases that A is odd or even.
The answer is 7 2
We know that each pair on consecutive numbers needs to be odd. What does that mean? Well, we know that
Even + Even = Even
Odd + Odd = Even
Odd + Even = Odd
(Easy to prove, proof left to reader)
Therefore we now know that the numbers beside each other (the ones that are consecutive) need to be of a different parity. This leads to the structure
A, B, C, D, E, F
even, odd, even, odd, even, odd
Working with this structure: Now we know that in the interval 1 to 6, there are 3 odd numbers to choose from {1, 3, 5} and 3 even numbers to choose from {2, 4, 6}. We also know that there are 3 even spots {A, C, E}, and 3 odd spots {B, D, F}.
This leads us to say to think how many ways are there to put 3 numbers into 3 spots for the evens. 3 ! (First hole, how many choices do we have? 3. Put one of these choices into the hole. How many choices now? 2. Put one of these into the second hole. How many choices now? 1. Put the last into the last hole. 3 × 2 × 1 = 3 ! )
We also know that are that 3 odd numbers to put into the 3 odd spots. 3 !
We multiply them together 3 ! × 3 ! to get how many ways to arrange the numbers for this structure. We're almost there...
Now that is just half of the arrangements. We also have to remember that you can arrange the odds and evens differently:
A,B,C,D,E,F
Even, Odd, Even, Odd, Even, Odd (First structure)
Odd, Even, Odd, Even, Odd, Even (Second structure)
So now we multiply by two
3 ! × 3 ! × 2 = 7 2
If we start from point A, we have 6 different options. Clearly, if the first is odd, the next should be even, and the same if the first is even. So, for the point B, we have 3 options. For C, 2 options, because point A has the same parity. Point D, 2 options, point E, 1 option and point F 1 option. So we have 6 x 3 x 2 x 2 x 1 x 1 = 72 ways.
Pick a , there are six ways to do it, then B , F need to have opposite parity, there are 3 ways to pick B and 2 ways to pick F (the order actually doesn't matter), then C , E need to have identical parity to A , hence there are two ways to pick C and one way to pick E , one way to pick D remains.
Hence the number sought is 6 × 3 × 2 × 1 × 2 × 1 = 7 2
;We must have odd even odd even odd even or even odd even odd even odd. In each case we must multiply by $3!^2$, so the answer is 2 6 ^=72
When the problem says the sum of two consecutive numbers must be odd, you immediately know that the pattern must be
odd-even-odd-even-odd-even ~OR~ even-odd-even-odd-even-odd.
The first point, (any point would be good as the points have circular symmetry) would have the choice to start with the odd numbers or the even numbers. So the starting point gets TWO CHOICES before it even chooses the number it would have. Then the starting point has THREE numbers to CHOOSE from. (1, 3, 5, or 2, 4, 6)
The same goes for the second point, it also has THREE CHOICES.
The third point gets one of the two numbers left over from the first point's choice, so it has TWO CHOICES.
Similarly, the fourth point gets one of the two numbers left over from the second point's choice, so it also has TWO CHOICES.
The fifth point gets the number left over from the first and third point's choice, so it only gets ONE CHOICE.
Similarly, the sixth point gets the number left over from the second and fourth point's choice so it only gets ONE CHOICE.
The numbers in caps are the number of choices: 2 ∗ 3 ∗ 3 ∗ 2 ∗ 2 ∗ 1 ∗ 1 which equals 7 2 .