Of circles, tangents, and triangles?
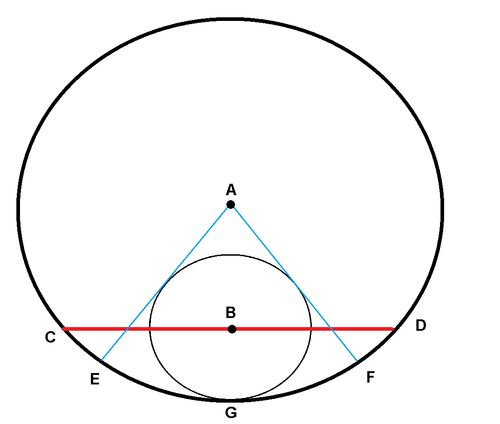 In the figure above, circle
is tangential to circle
at
.
is perpendicular to
, intersecting at
. The length of
is three times the diameter of circle
. Radii
and
are drawn such that they are tangential to circle
. If
can be expressed in the form of
where
and
are coprime positive integers,
In the figure above, circle
is tangential to circle
at
.
is perpendicular to
, intersecting at
. The length of
is three times the diameter of circle
. Radii
and
are drawn such that they are tangential to circle
. If
can be expressed in the form of
where
and
are coprime positive integers,
determine .
The answer is 56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
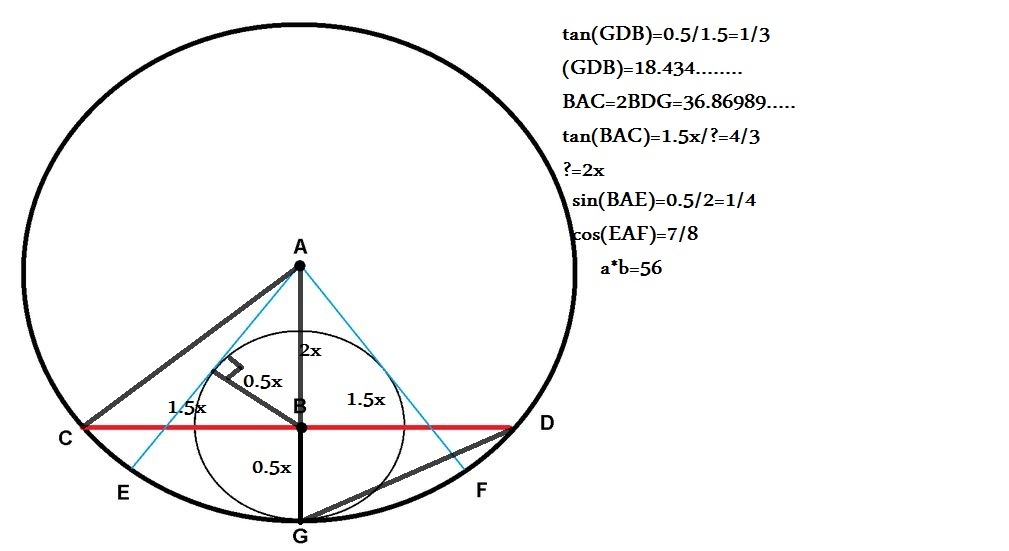
Let R be the radius of circle A , and r be the radius of circle B . Since C D = 6 r , it follows that B D = 3 r . By Pythagorean Theorem, we can determine the length of the radius of circle A , which would be essential in determining ∠ F A E .
( B D ) 2 + ( A B ) 2 = ( A D ) 2
( 3 r ) 2 + ( R − r ) 2 = R 2
9 r 2 + R 2 − 2 R r + r 2 = R 2
1 0 r 2 = 2 R r
R = 5 r .
By establishing that, we now draw a segment from B to the point of tangency of A F . We let this point be P . We can now get θ = ∠ P A B . That is,
s i n ( θ ) = A B B P = R − r r
s i n ( θ ) = 4 1
Our objective is to get ∠ F A E , which is equal to 2 θ . Using the double angle identity for cosine, we get
c o s ( 2 θ ) = 1 − 2 s i n 2 ( θ )
c o s ( 2 θ ) = 1 − 2 ( 4 1 ) 2
c o s ( 2 θ ) = 1 − 8 1
c o s ( 2 θ ) = 8 7
And so we find ∠ F A E = c o s − 1 ( 8 7 ) .
using a = 7 and b = 8 , we find that a × b = 5 6