Off Center Angle
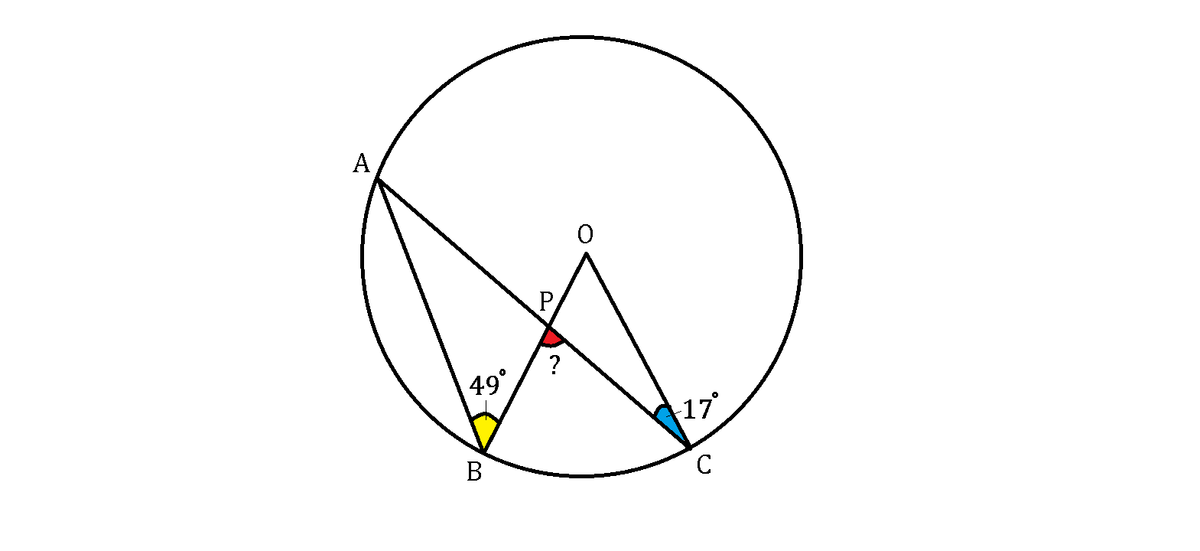
The points A , B , C are on a circumference, where O is the center, and P is the intersection point of A C and B O , as shown above.
If ∠ A B P = 4 9 ∘ and ∠ P C O = 1 7 ∘ , what is the value of ∠ B P C in degrees?
The answer is 81.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
@Worranat Pakornrat Hats off , sir !👌🙇
Sorry, I really find this confusing... only if someone had a video in this
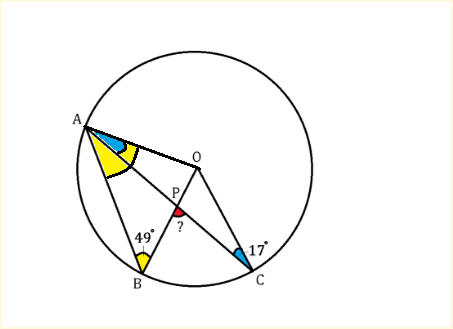
Joining OA, We see that both the blue angles are equal and so are the 2 yellow angles. (By isoceles triangle theorem since radii are equal)
So , Using exterior angle theorem in triangle P A B , We get R e d = 2 Y e l l o w − B l u e
Thus R e d = 2 ∗ 4 9 − 1 7 = 9 8 − 1 7 = 8 1
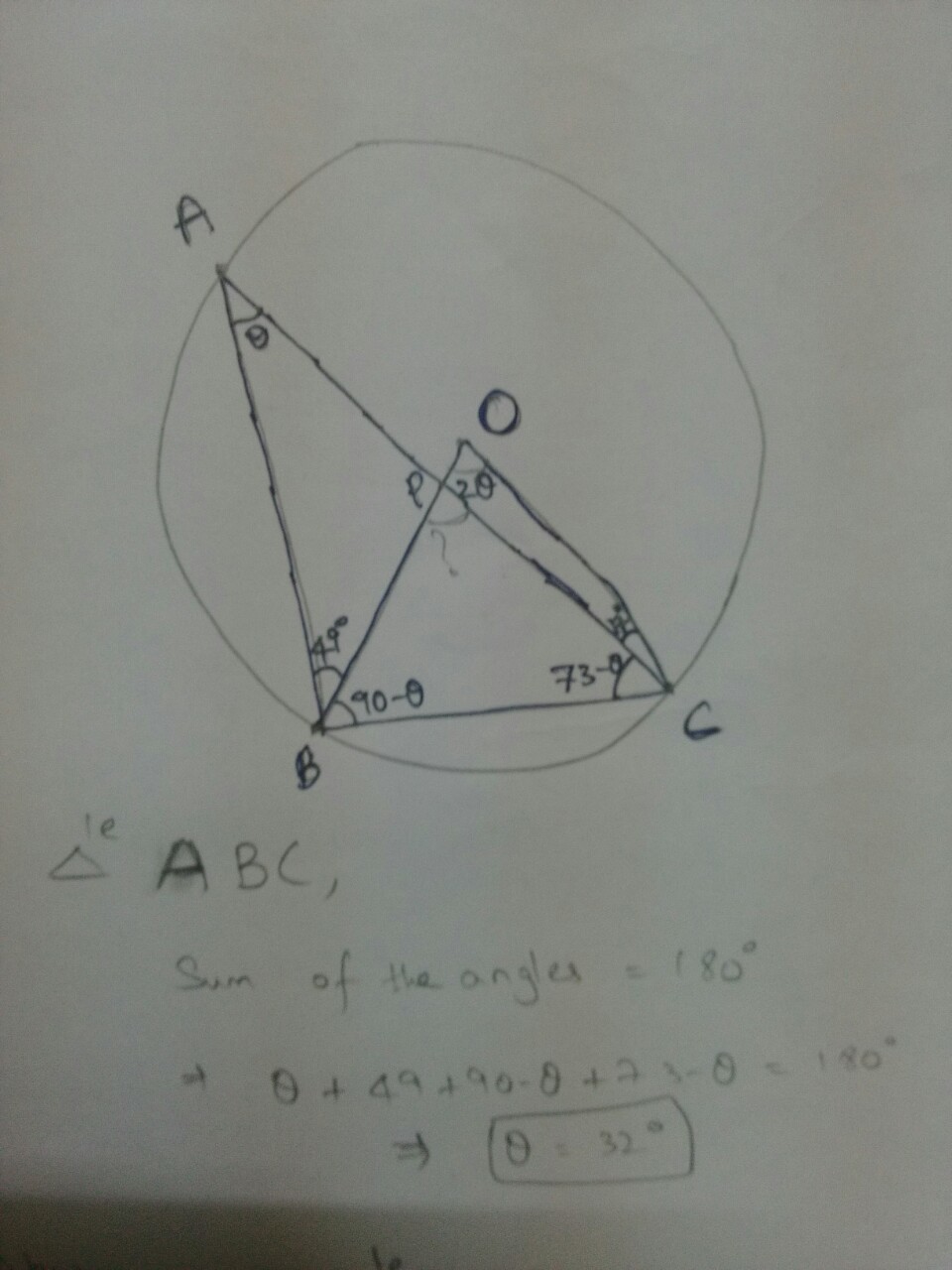

Upper image for diagram
Lower image for solution.. easy to understand
1) OBC Is an isosceles triangle.
2) 2(Angle BAC) = Angle BOC.
Let us take Angle BAC=θ.
So angle BOC =2θ.
Took me a few mins how you got 90 - theta and 72 - theta, but that's from your last remark :) nice solution.
Actually it is 73-theta , not 72 - theta @Peter van der Linden
Since BAP and BOC cut the same arc, BAP = 1/2 * BOC
BPC = BAP + 49 = BOC + 17 because an exterior angle = sum of the two non adjacent angles
Substituting 1/2*BOC + 49 = BOC + 17
Solving BOC = 64
64 + 17 = 81 degrees
Since ∠ A P B + ∠ B P C = 1 8 0 ∘ , then ∠ B P C = ∠ B A P + ∠ A B P = ∠ B A P + 4 9 ∘ .
Thus, we are attempting to find ∠ B A P for a solution, and we can do so by extending the O C line to meet point D on the circumference before joining it with point B , as shown below: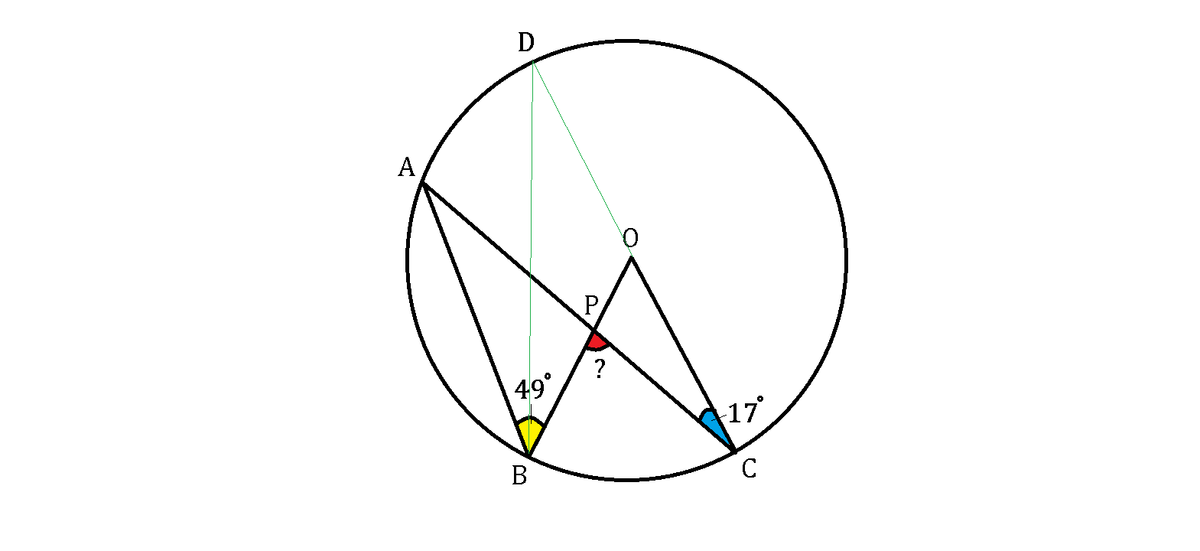
According to Inscribed Angles Theorem , ∠ B A P = ∠ B D O , and because △ B D O is an isosceles triangle, ∠ D B O = ∠ B D O .
Furthermore, from Inscribed Angles Theorem , ∠ A B D = ∠ A C D = 1 7 ∘ .
Thus, ∠ A B P = 4 9 ∘ = ∠ A B D + ∠ D B O = 1 7 ∘ + ∠ B A P .
Hence, ∠ B A P = 4 9 ∘ − 1 7 ∘ = 3 2 ∘ .
Finally, ∠ B P C = 4 9 ∘ + 3 2 ∘ = 8 1 ∘ .