Off-tune tuning fork
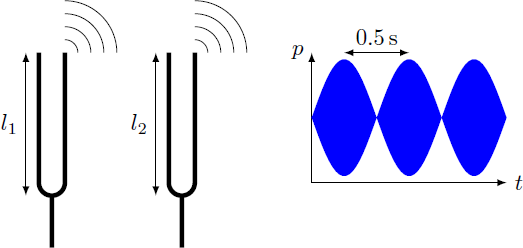
Two tuning forks with slightly different lengths and are vibrated simultaneously. Because their vibration frequencies differ, an acoustic beating is created, so that the sound gets loud and quiet twice a second. What is the natural frequency of the longer tuning fork in units of hertz?
The answer is 402.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The natural vibrations of the tuning forks are standing waves with sound velocity c = λ f . For the fundamental vibration, the wavelength is λ = 4 l , since the top corresponds to anti-node at and the bottom corresponds to a node, so that the oscillation frequency is f = 4 1 c / l .
The superimposition of two sine waves with the frequencies f 1 and f 2 results sin ( 2 π f 1 t ) + sin ( 2 π f 2 t ) = sin ( π ( f + + f − ) t ) + sin ( π ( f + − f − ) t ) = [ sin ( π f + t ) cos ( π f − t ) + cos ( π f + t ) sin ( π f − t ) ] + [ sin ( π f + t ) cos ( π f − t ) − cos ( π f + t ) sin ( π f − t ) ] = 2 sin ( π f + t ) cos ( π f − t ) with f + = f 1 + f 2 and f − = f 1 − f 2 . The result is a sine wave with the mean frequency f + / 2 whose amplitude is modulated by a cosine oscillation with the frequency f − / 2 . This phenomenon is also called (acoustic) beating.
The amplitude is maximized for the times t = n / f − = n Δ t , n = 0 , 1 , 2 , … , so that Δ t = 0 . 5 s yields a difference frequency f − = 2 Hz . It follows f − ⇒ c ⇒ f 1 = 4 c ( l 1 1 − l 2 1 ) = l 1 1 − l 2 1 4 f − = 4 l 1 c = 1 − l 2 l 1 f − = 4 0 2 Hz