O Christmas Tree

Electricity and Magnetism Level 2

A wire is bent into the shape of a Christmas tree, as shown below. The wire has a resistance of 1 Ω 1 \, \Omega per unit length. A voltage of 100 V 100 \, V is applied between the red and green points at the base of the tree.

How many amps of current flow through the wire?

Note: The voltage source (not pictured) completes the circuit to provide a closed path for the current


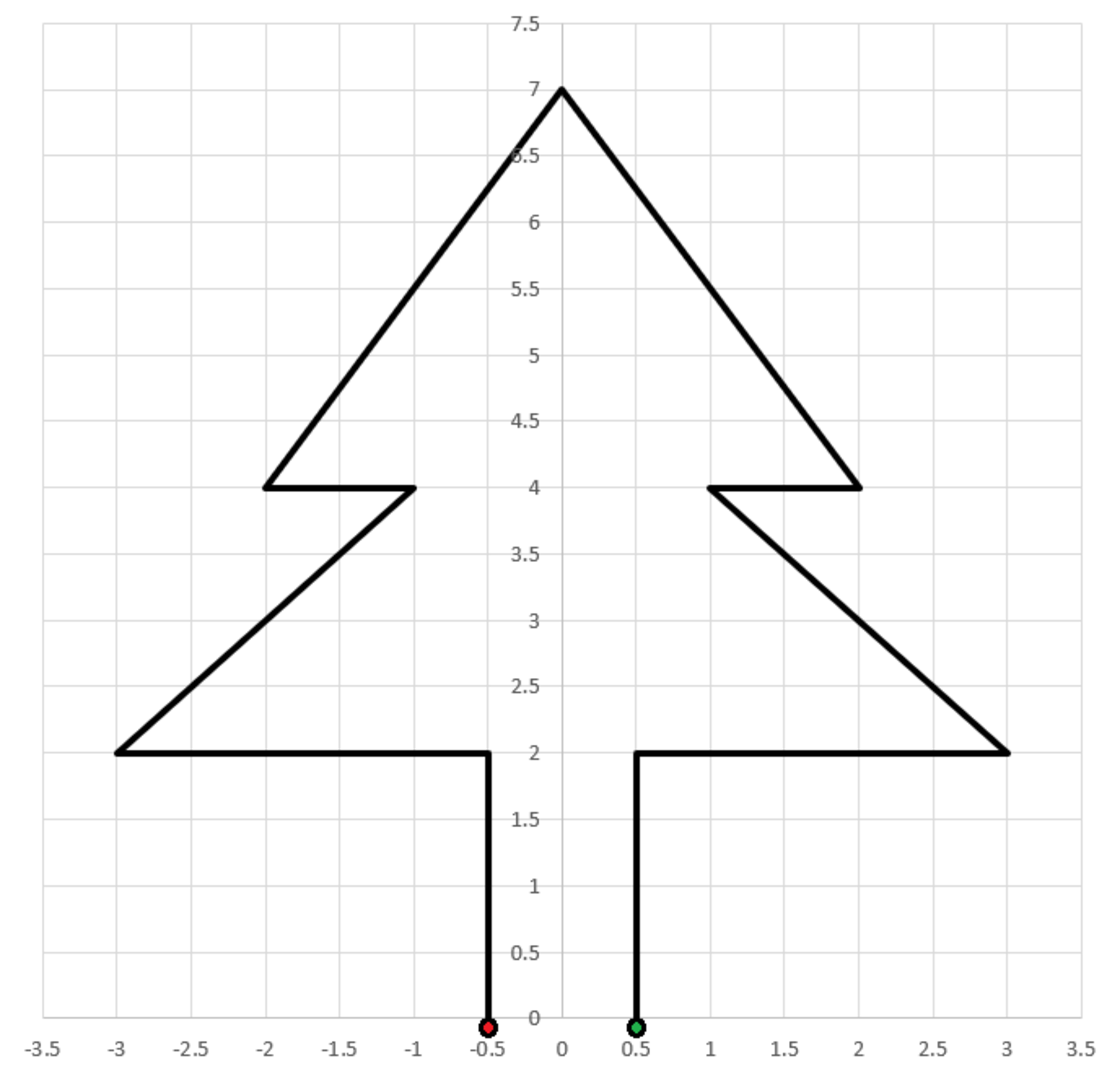
The answer is 4.1897.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Otto Bretscher
Dec 25, 2018

Oh Tannenbaum! I got it on the third and last attempt; those half-units of length are tricky! ;)

The length of the wire is 2 ( 2 + 2.5 + 8 + 1 + 13 ) ≈ 23.87 2(2+2.5+\sqrt{8}+1+\sqrt{13})\approx 23.87 meters. By Ohm's Law, the current is I = V R ≈ 4.1897 I=\frac{V}{R}\approx \boxed{4.1897} amps

Merry Christmas to you, Steven!

0 Helpful 0 Interesting 2 Brilliant 0 Confused

I had to look up Ohm's law to make sure of the formula. Really it's just a simple geometry problem.

Jeremy Galvagni - 2 years, 5 months ago

I = V R \frac{V}{R}

I = V o l t a g e w i r e l e n g t h × r e s i s t a n c e p e r u n i t \frac{Voltage}{wire length \times resistance per unit}

I = 100 V 23.86795 × 1 \frac{100V}{23.86795 \times 1}

=4.189 A

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...