A nice result
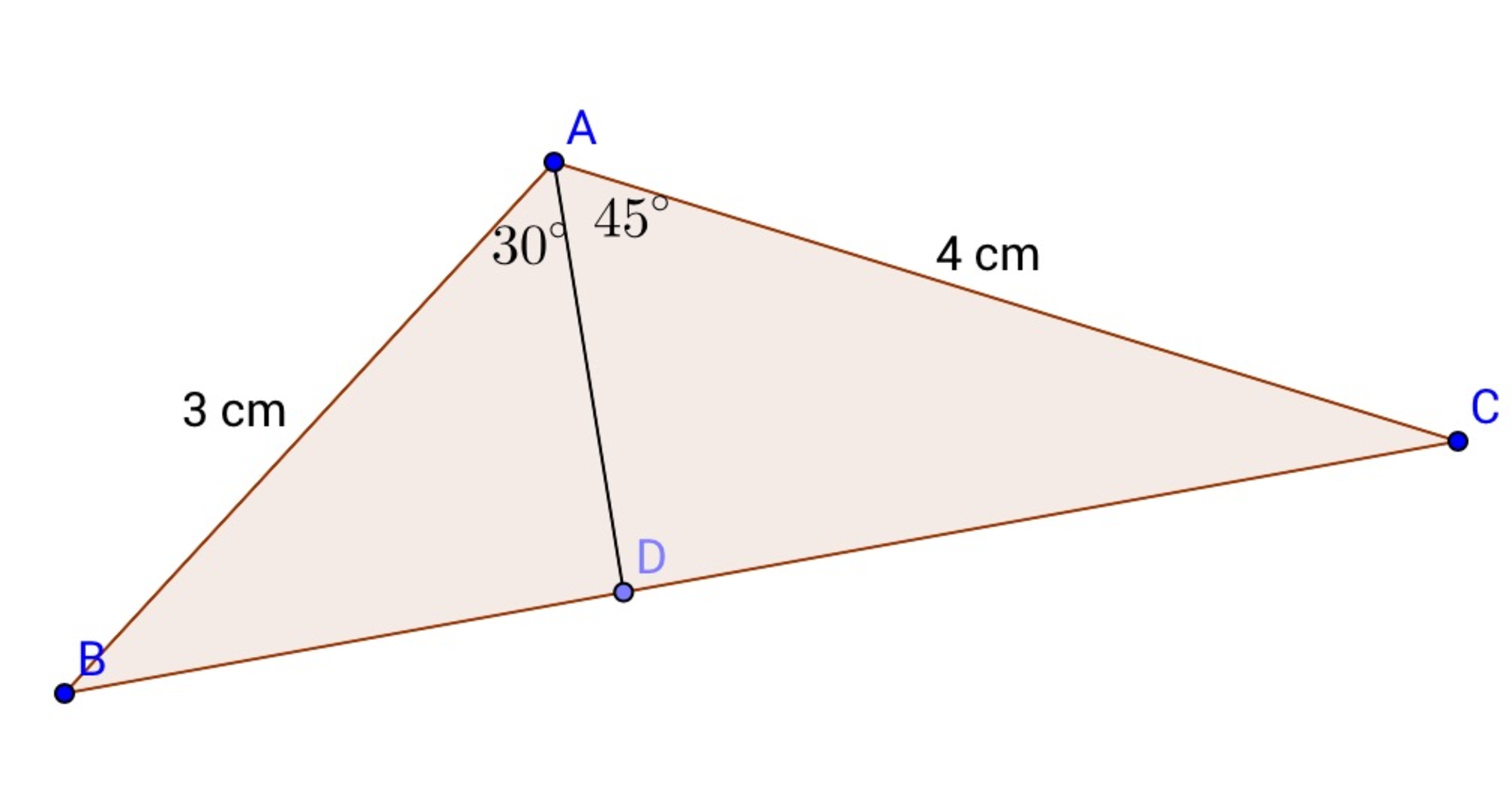
In the above figure, find the length of A D to an accuracy of 5 decimal places.
Note : Figure above is not to scale.
The answer is 2.6779.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
Good observation to be aware of.
Yay! Even I used your result :P
Thanks for the note! It took quite a bit of time with trig and angle chasing, so that is really cool to see the more elegant approach.
By cosine law on △ A B C , we have
B C 2 = 3 2 + 4 2 − 2 ( 3 ) ( 4 ) ( cos 7 5 )
B C ≈ 4 . 3 3 4 5 5 2 2 1 6
By sine law on △ A B C , we have
4 sin B = 4 . 3 3 4 5 5 2 2 1 6 sin 7 5
B ≈ 6 3 . 0 4 6 3 0 2 0 6 ∘
Thus, ∠ A D B = 1 8 0 − 3 0 − 6 3 . 0 4 6 3 0 2 0 6 ≈ 8 6 . 9 5 3 6 9 7 9 4 ∘
By sine law on △ A B D , we have
sin 6 3 . 0 4 6 3 0 2 0 6 A D = sin 8 6 . 9 5 3 6 9 7 9 4 3
A D ≈ 2 . 6 7 7 9 0
Area Tr. ABC = Area Tr. BAD + Area Tr, CAD. Hence, (1/2) 3 4 sin(75)=(1/2)[3 x sin(30)+4 x*sin(45)] or x= 6(√2+√6)/(3+4√2) or x ~= 2.6779 cm
(1) Compute BC by Law of Cosines. (2) Compute total area by Herron's formula. (3) Compute total area by A = (1/2)(AD)[((AB)sin(30) + (AC)sin(45)). Equate the expressions for area and solve for AD. Ed Gray
Found out BC by Cos Law. Repeatedly used Sin Law to get angle DCA and hence angle ADC; then with AC given got AD. It is just the normal way. Karthik Venkata's formula is really very helpful.
Use this . You will find that A D = 4 2 + 3 6 2 ( 3 + 1 ) .