Oh! Snails

Classical Mechanics Level 3

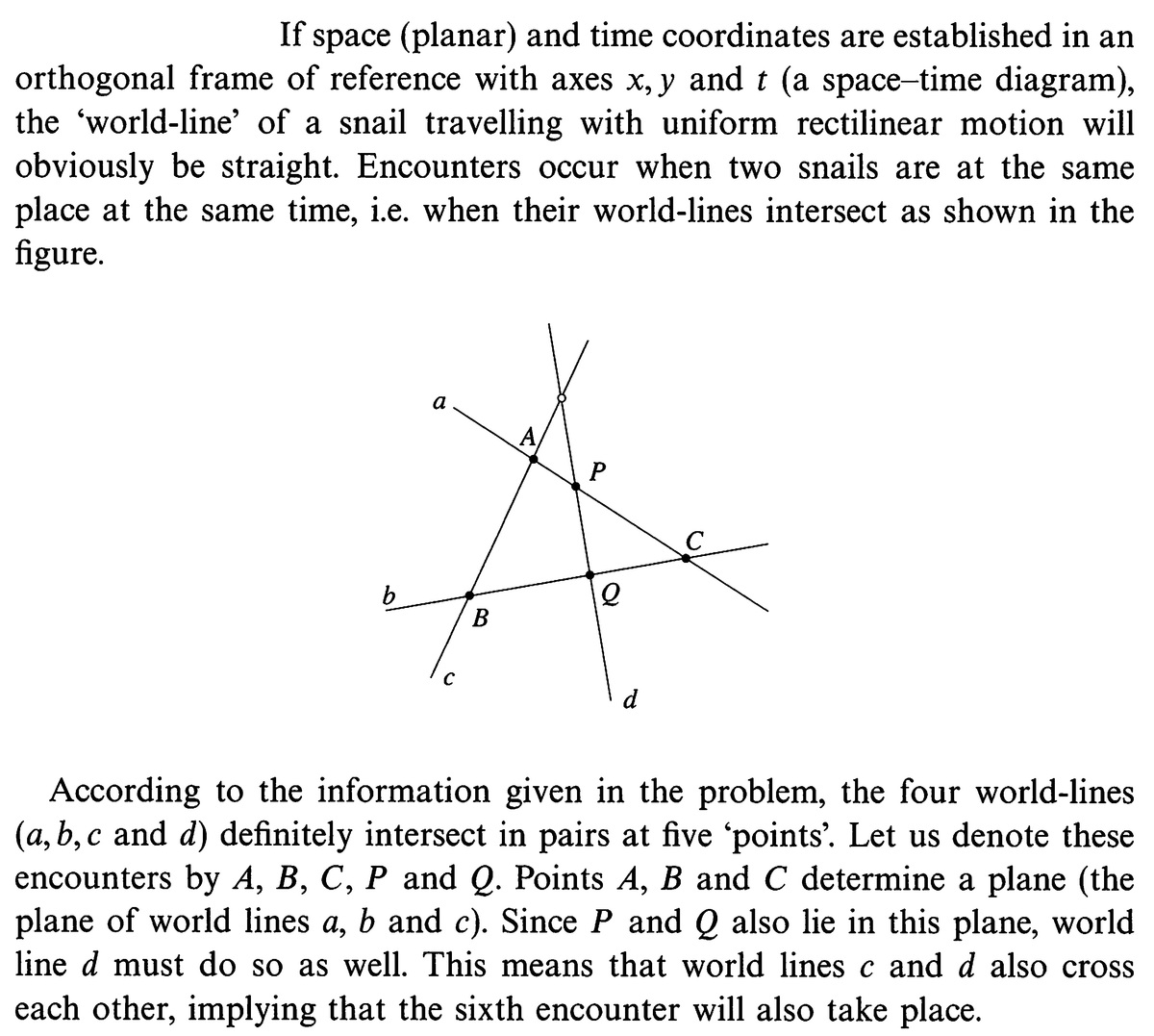
Four snails travel at uniform, rectilinear motion on a very large plane surface. The directions of their paths are random, (but not parallel, i.e. any two snails could meet), but no more than two snail paths can cross at any one point. Five of the ( 4 × 3 ) / 2 = 6 (4\times3)/2=6 possible encouters have already occured. Can we state with certainty that the sixth encounter will also occur?

This question is not original.
No Yes

Jyotisman Das by Jyotisman Das , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Jyotisman Das
Jan 26, 2016

There are two solutions:

First One:

Second One:

1 Helpful 0 Interesting 0 Brilliant 0 Confused

In the first solution once u proved all three move in same line w.r.t. alpha...then...say the other three as in order of their distance from alpha ..are beta..then gamma.. then delta..now forget alpha...and chose beta as point of reference ... for two more collisions to occur ..delta and gamma must have some relative velocity...w.r.t. beta and collide at some instance but how can u prove that these two will have a relative velocity to each other which will decrease their separation for 6th collision to take place.. 😓.pls clear my doubt.

PRANAV Singla - 3 years, 4 months ago
K T
Jul 11, 2019

By representing time as the third dimension, the problem boils down to geometry in R 3 \mathbb{R}^3 . Each encounter in this space/time is an event, which is represented by a point. Each snail path through space and time is represented by a straight line. Supposing we have snails a,b,c and d, and that the only encounter that has not (yet ) occurred is that between c and d, notation: (cd). The encounters (ab), (bc) and (ca), define a plane, and the paths of a, b and c all lie in this plane. The encounters (ad) and (bd) then must lie in the same plane and therefore the path of d must also lie in this same plane, so that the lines of c and d are in the same plane and they intersect at some point in that plane (in space time). Unless they are parallel, which was not the case. So there will be an encounter (cd). The meaning of this is that c and d will be simultaneously be at the same position, in other words: they will meet.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...