Old exciting formula!
2 i ln ( 1 + i 1 − i )
Which of the options is a value of the expression above.
Notation: i = − 1 denotes the imaginary unit .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
z = 2 i ln ( 1 + i 1 − i ) = 2 i ln ( ( 1 + i ) ( 1 − i ) ( 1 − i ) 2 ) = 2 i ln ( 2 − 2 i ) = 2 i ln ( − i ) = 2 i ln ( e − 2 π i ) = 2 i ( − 2 π i ) = π Consider only the principal value and by Euler’s formula: e θ i = cos θ + i sin θ
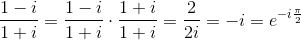
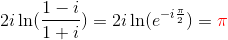
We have 1 + i 1 − i = − i = e π i ( − 2 1 + 2 n ) , for any integer n
Therefore, 2 i ln ( 1 + i 1 − i ) = 2 i ⋅ ( π i ( − 2 1 + 2 n ) ) = ( 1 − 4 n ) π
We select the branch given by n = 0 to get an answer of π (also note that none of the other answers is an integer multiple of π , so they cannot be correct).
NOTE AND WARNING: The complex logarithm is multi-valued, so it only makes sense to say that it equals a particular value on a given branch, not in general. In particular, unless you are equipped to deal with a multi-valued logarithm, most of the standard properties of the real logarithm do not hold for the complex logarithm.