Olympiad Corner 3
⎩ ⎪ ⎨ ⎪ ⎧ x + x y + x y z = 1 2 y + y z + x y z = 2 1 z + z x + x y z = 3 0
Given that x , y and z are real numbers that satisfy the system of equations above, find the sum of all possible values of x + y + z .
Give your answer to 3 decimal places.
The answer is 15.707.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I would like to know where I got it wrong. In your equations of x, y and z, I put k = 1 to get x, y, and z as 4/7, 7/10 and 5/2 giving me a perfect k = xyz = 1. But, it does not satisfy your original equations. That means that these three equations have an inherent fault which results in an invalid answer. Where is the fault?
Log in to reply
Sir, from the equations we find that the values of x,y,z depend upon the value of xyz so evaluating the equation by a preset value of xyz would provide solutions which might be incompitable with the original equation.
Log in to reply
'Preset' is a misnomer here. I solved for all possible xyz to get 1, 10, 27 and 28 as solutions. Then why is 1 singled out for giving wrong results.
Can you suggest some more problem of the same type ?
F
r
o
m
t
h
e
t
h
i
r
d
e
q
u
a
t
i
o
n
,
Z
=
1
+
X
+
X
Y
3
0
.
S
u
b
s
t
i
t
u
t
i
n
g
t
h
i
s
v
a
l
u
e
i
n
f
i
r
s
t
t
w
o
e
q
u
a
t
i
o
n
s
,
X
(
1
+
Y
(
1
+
1
+
X
+
X
Y
3
0
)
)
−
1
2
=
0
.
Y
(
1
+
1
+
X
+
X
Y
3
0
(
‘
1
+
Y
)
)
−
2
1
=
0
.
T
h
i
s
w
a
s
g
r
a
p
h
e
d
.
T
h
r
e
e
p
o
i
n
t
s
o
f
i
n
t
e
r
s
e
c
t
i
o
n
s
w
e
r
e
o
b
t
a
i
n
e
d
a
s
s
h
o
w
n
o
n
t
h
e
g
r
a
p
h
.
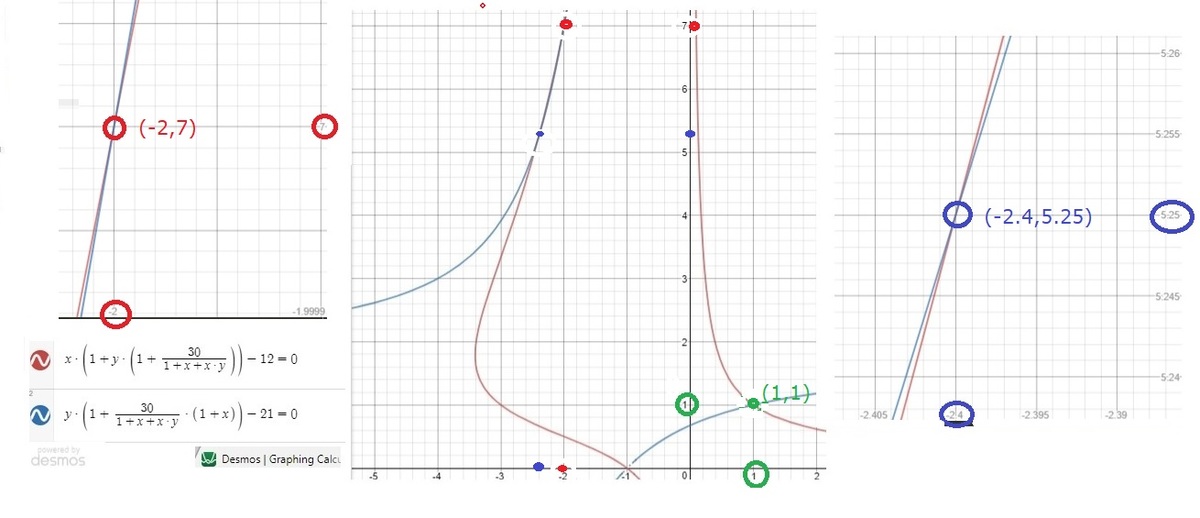
Z
w
a
s
f
o
u
n
d
u
s
i
n
g
t
h
e
t
h
r
e
e
x
−
y
v
a
l
u
e
s
.
T
h
e
r
e
s
u
l
t
.
.
.
(
1
,
1
,
1
0
)
;
(
−
2
,
7
,
−
2
)
;
(
−
2
.
4
,
5
.
2
5
,
−
2
.
1
4
2
8
)
A
d
d
i
n
g
t
h
e
s
e
n
i
n
e
n
u
m
b
e
r
s
=
1
5
.
7
0
7
2
.
x+xy+xyz=12
y+yz+xyz=21
z+zx+xyz=30
Now multiply the first equation by z and subtract from the third equation, multiply the second equation by x and subtract from the first and similarly multiply the third equation by y and subtract from the second equation to get,
(13z - 30)/z = (22x - 12)/x = (31y - 21)/y = xyz = k
Now,
x = (12)/(22-k),
y = (21)/(31-k),
z = (30)/(13-k).
Put these values of x,y,z in the first equation to get,
[k^(3)] - [65 (k^(2))] + 1306k - 7560 = 0
We get the solutions k = 10,27,28.
For each of these we get,
(x,y,z) = (1,1,10)
Whose sum =15.707