Olympiad Geometry : Viviani, Ptolemy and INMO 1995
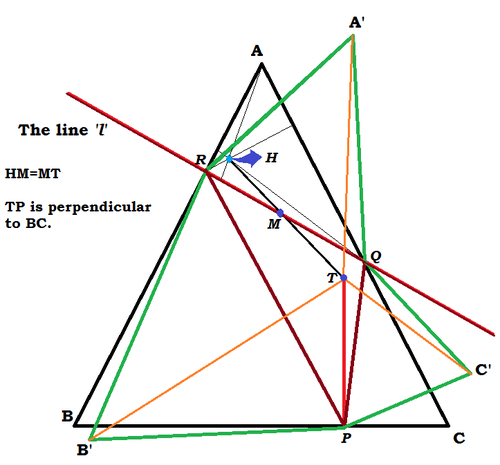 Suppose a line
'l'
cuts an equilateral triangle
of side
in two points different from the vertices. Say it cuts
and
in points
and
respectively. We mark the orthocentre
of the triangle
and also the midpoint
of side
. We extend
to a point
so that
. The point
is the foot of perpendicular from
on side
.
Suppose a line
'l'
cuts an equilateral triangle
of side
in two points different from the vertices. Say it cuts
and
in points
and
respectively. We mark the orthocentre
of the triangle
and also the midpoint
of side
. We extend
to a point
so that
. The point
is the foot of perpendicular from
on side
.
Now, we draw outward equilateral triangles , , and . (The Napoleonic triangles of triangle ).
The task is to find: .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A slight generalization of the I N M O 1 9 9 5 result is very often used in many Olympiad geometry problems around the world. To quote:
I leave the proof to you, it is simple angle-chasing. Although, the proof of the converse (which is almost the same proof actually !) can be found in the solution to this another problem by me.
The above result powerfully tells us that since T A is diameter of circumcircle of Δ A Q R , ∡ T Q A = 9 0 and also ∡ T R A = 9 0 .
In other words, P , Q and R are feet of perpendiculars from T to the sides of equilateral triangle A B C . So, applying the Viviani's theorem we have:
Now, observe that quadrilateral T R B P is cyclic.( ∡ T R B = ∡ T P B = 9 0 ). So, ∡ R T P = 1 2 0 . So, even quadrilateral T R B ′ P will be cyclic. (Opposite angles will sum to 6 0 + 1 2 0 = 1 8 0 ). So, apply Ptolemy's theorem on the quadrilateral T R B ′ P , denoting B ′ R = B ′ P = P R = a :
B ′ T × a = R T × a + T P × a ⟹ B ′ T = R T + T P .
Similiarly, we obtain:
C ′ T = P T + T Q
A ′ T = Q T + T R
And adding,
A ′ T + B ′ T + C ′ T = 2 × ( R T + P T + Q T ) = 3 × A B = 3 .
(From the result (*) above and since A B = 3 )