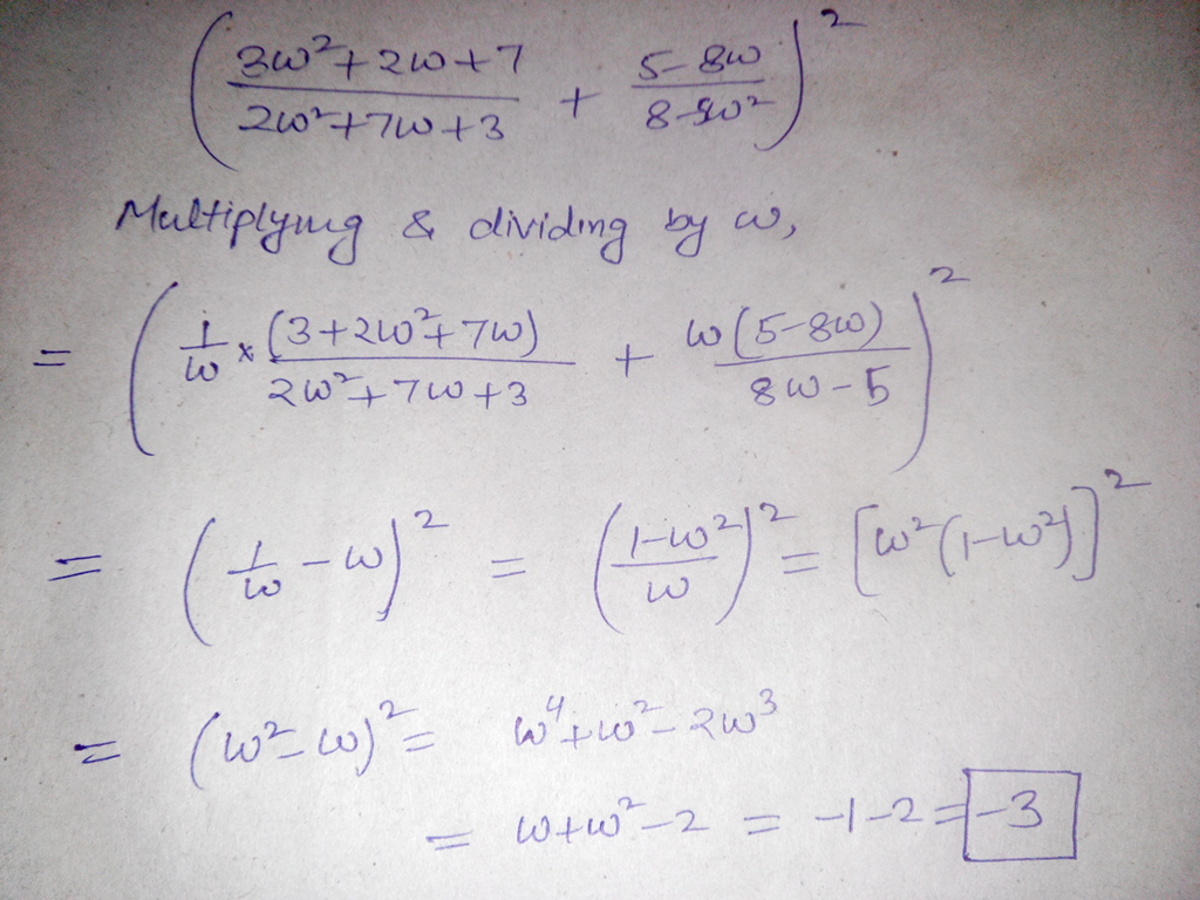Omega
X = ( 2 ω 2 + 7 ω + 3 3 ω 2 + 2 ω + 7 + 8 − 5 ω 2 5 − 8 ω ) 2
Find the value of X
Hint: ω and ω 2 are two of the cubic roots of 1
The answer is -3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
since ω is a cubic root of 1 therefore ω 3 = 1
In this step, I multiplied certain terms by 1 :
X = ( 2 ω 2 + 7 ω + 3 3 ω 2 + ( 2 ω × 1 ) + ( 7 × 1 ) + 8 − 5 ω 2 ( 5 × 1 ) − 8 ω ) 2
now substitute the ones by ω 3 :
X = ( 2 ω 2 + 7 ω + 3 3 ω 2 + 2 ω 4 + 7 ω 3 + 8 − 5 ω 2 5 ω 3 − 8 ω ) 2
Take ω 2 common factor from the first fraction and take − ω from the second fraction so we have:
X = ( 2 ω 2 + 7 ω + 3 ω 2 ( 3 + 2 ω 2 + 7 ω ) + 8 − 5 ω 2 − ω ( 8 − 5 ω 2 ) ) 2
= ( ω 2 − ω ) 2
= ( ± 3 i ) 2 = 3 i 2 = − 3
if ω^3 = 1
ω^3 - 1 = 0
( ω - 1 ) ( ω^2 + ω + 1 ) = 0
ω = 1 or ω^2 + ω + 1 = 0
Then why I get wrong , when I apply ω = 1 to the equation ?
you should have told that ω is a complex cubic root
Log in to reply
it was mentioned that w and w^2 are cubic roots of unity, which means they are the two complex cube roots of unity
Since ω and ω 2 are cubic roots of 1 , ⇒ ω 2 + ω + 1 = 0 ⇒ ω 2 = − ω − 1
Therefore,
X = ( 2 ω 2 + 7 ω + 3 3 ω 2 + 2 ω + 7 + 8 − 5 ω 2 5 − 8 ω ) 2
= ( − 2 − 2 ω 2 + 7 ω + 3 − 3 − 3 ω + 2 ω + 7 + 8 + 5 + 5 ω 2 5 − 8 ω ) 2
= ( 1 + 5 ω 4 − ω + 1 3 + 5 ω 5 − 8 ω ) 2
= ( ( 5 − 8 ω ) ( 1 3 + 5 ω ) ( 4 − ω ) ( 1 3 + 5 ω ) + ( 1 + 5 ω ) ( 5 − 8 ω ) ) 2
= ( ( 1 3 + 7 0 ω + 2 5 ω 2 ) ( 5 2 + 7 ω − 5 ω 2 ) + ( 5 + 1 7 ω − 4 0 ω 2 ) ) 2
= ( − 1 2 + 4 5 ω ( 5 7 + 1 2 ω ) + ( 4 5 + 5 7 ω ) ) 2 = ( − 4 + 1 5 ω ( 1 9 + 4 ω ) + ( 1 5 + 1 9 ω ) ) 2
= ( − 4 + 1 5 ω 3 4 + 2 3 ω ) 2 = 1 6 − 1 2 0 ω + 2 2 5 ω 2 1 1 5 6 + 1 5 6 4 ω + 5 2 9 ω 2
= − 2 0 9 − 3 5 5 ω 6 2 7 + 1 0 3 5 ω = − ( 2 0 9 + 3 5 5 ω ) 3 ( 2 0 9 + 3 5 5 ω ) = − 3
Slight calculation errors put me off the track in the end :(
Though a long solution can be shortened as below, the solutions by multiplication and division by
ω
is by far better.
ω
2
+
ω
=
−
1
,
ω
2
−
ω
=
−
3
i
.
2
ω
2
+
1
=
=
−
3
i
,
2
ω
+
1
=
+
3
i
No need of doing complex maths just try to make numerator like denominator. Yes you only need to remember certain properties likeΠw³=1 andw²=1÷w(can't find omega on keypad