On A Lattice: Part 1
A lattice is the coordinate plane with only points that have integer coordinates. Ex: (2,3) is a lattice point, but (4,6.3) is not.
Is it possible to draw an equilateral triangle with vertices on the lattice?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let ABC be the triangle wth B and C lattice points, BC horizontal. So A would be at a vertical distance of root(3) * BC. There is no Lattice point there. If BC is at any angle , atan(1/n), where n is any integer, there is no lattice point at a ditance of root(3) *BC perpendicular to BC to locate A. Note perpendicular to BC should be from Midpoint of BC, but even any point at that Distance is not a lattice point.
Assume 3 vertices of an equilateral triangle are lattice points, and call them ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) (listing in counter-clockwise direction)
Therefore, the area of the triangle is 2 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ x 1 x 2 x 3 x 1 y 1 y 2 y 3 y 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ = 2 1 [ x 1 y 2 + x 2 y 3 + y 3 x 1 − x 2 y 1 − x 3 y 2 − x 1 y 3 ] which obviously is an integer or a number end with . 5 (or, a rational area, at least)
Let's call d be the side of the equilateral triangle
Hence, d 2 = ( x i − x j ) 2 + ( y i − y j ) 2 , i = j , 1 ≤ i , j ≤ 3 which apparently is an integer (since all 3 points are lattice points)
Thus, the area of the triangle is 2 1 d 2 s i n 3 π = 4 3 d 2
which is not a rational number at all
Therefore, the first assumption leads us to a contradiction, and we can conclude that no 3 lattice points can form an equilateral triangle
Assume that it is possible to draw an equilateral triangle with all vertices on the lattice.
Then for each side s , s 2 is a rational number as a hypotenuse solution to Pythagorean's Theorem with integer side lengths, and since the area of an equilateral triangle is A = 4 3 s 2 , it is an irrational number ( 3 ) times a rational number ( 4 s 2 ) which means the area must be irrational.
However, by Pick's Theorem all lattice polygons have an area of A = I + 2 1 B − 1 (where I is the number of points inside the polygon and B is the number of points on the boundary of the polygon) which means the area must rational.
Hence we have a contradiction (that the area must be both irrational and rational) which means our assumption (that it is possible to draw an equilateral triangle with all vertices on the lattice) is false .
Let us say it were possible, and call the triangle A . Call the three vertices of the equilateral triangle ( a , b ) , ( c , d ) , ( e , f ) , where a , b , c , d , e , f are integers. Now, we can draw a rectangle around triangle A so that the three vertices of A lie on the sides of the rectangle, similar to this, except the central triangle is equilateral (Google didn't have any of those).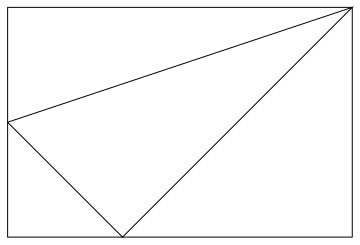
Now the rectangle has been decomposed into 4 triangles, one being equilateral, and the other three being right triangles. Call these three triangles Q , R , S . Now, Q , R , S have integer base lengths, since they are part of the lattice. This means that each of triangles Q , R , S has rational area, since they are right triangles and their area is given by 0 . 5 ∗ b h , which is rational when b and h are integers. The entire rectangle also has rational area, due to the fact that its base and height are integers. Now, we know that the sum of the areas of triangles A , Q , R , S is equal to the area of the rectangle, that is
A r e a ( A ) + A r e a ( Q ) + A r e a ( R ) + A r e a ( S ) = A r e a ( R e c t a n g l e )
Now we know that A r e a ( Q ) , A r e a ( R ) , A r e a ( S ) , and A r e a ( R e c t a n g l e ) are all rational, and therefore, A r e a ( A ) must be rational as well. But the area of any equilateral triangle with integer side lengths is irrational.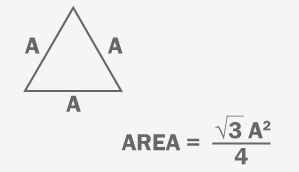
When the square of the side length is an integer (as it always is, due to the fact that the side is the hypotenuse of a right triangle with integer side lengths), the factor of r o o t ( 3 ) , which is irrational, causes the whole area to be irrational.
We now have a contradiction, which implies that you cannot put an equilateral triangle on a lattice.