On A Lattice: Part 3
Geometry
Level
3
Is it possible to place a regular hexagon on a lattice?
Yes, it is possible
No, it is not possible
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Assume we can.
First, we recognize that a regular can be decomposed into polygons of rational area in the following way.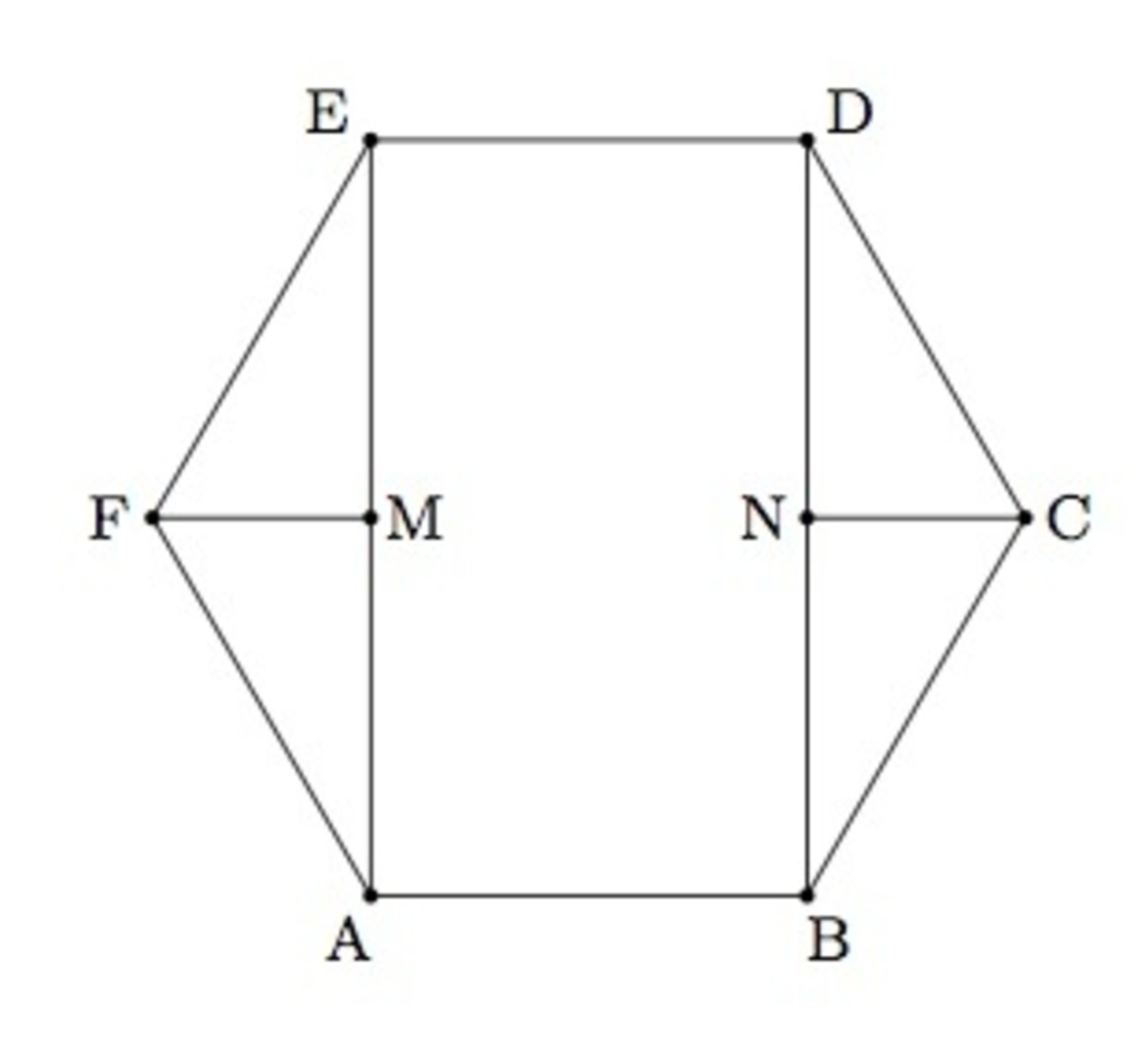
Because it is on a lattice, the segments EA, DB, FM, NC, in the picture have rational length, and so each polygon has rational area due to the fact that they are all right triangles or a rectangle. This implies that the hexagon has rational area.
Next we notice that the hexagon can be decomposed like this: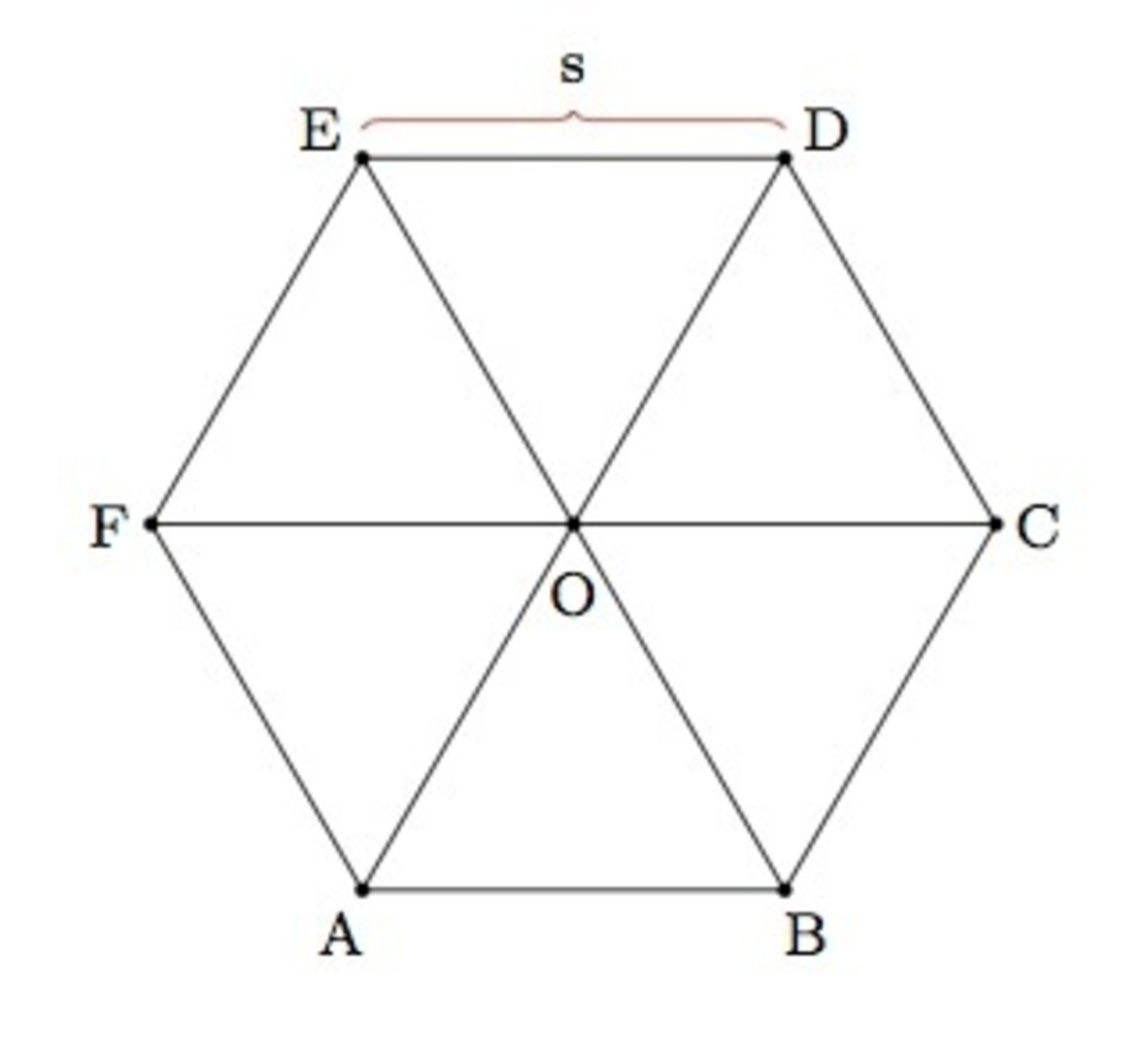
These are six equilateral triangles. Each of the equilateral triangles has irrational area, as the side length is an integer. Therefore, the sum of the six areas must be irrational as well. This implies that the hexagon has irrational area.
We now have a contradiction, meaning that you cannot put a regular hexagon on a lattice.