Perimeters!
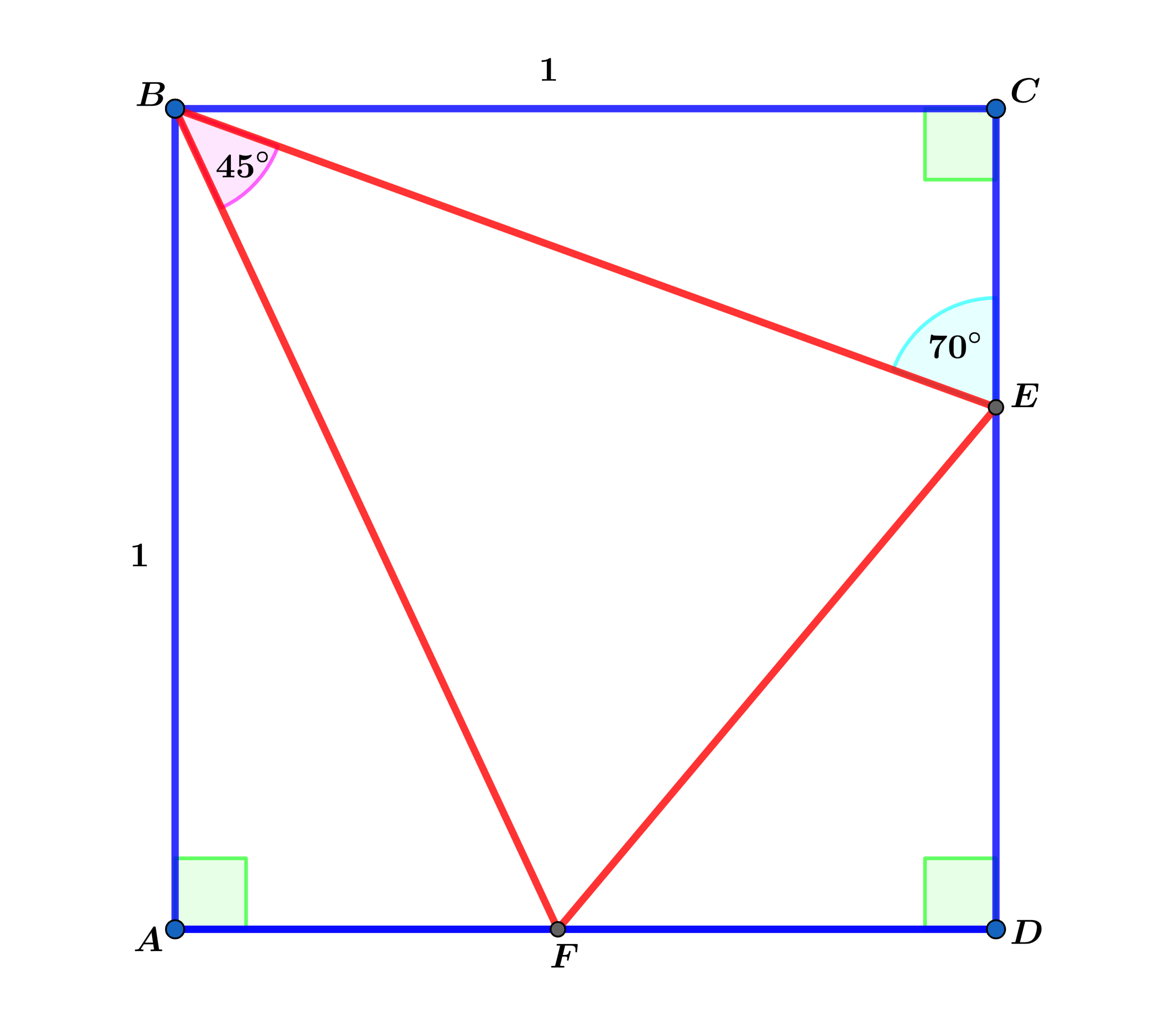
In the diagram above, square A B C D has a side length of 1 and the inscribed △ F B E has m ∠ F B E = 4 5 ∘ and the m ∠ B E C = 7 0 ∘ .
Find the perimeter of △ F E D .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
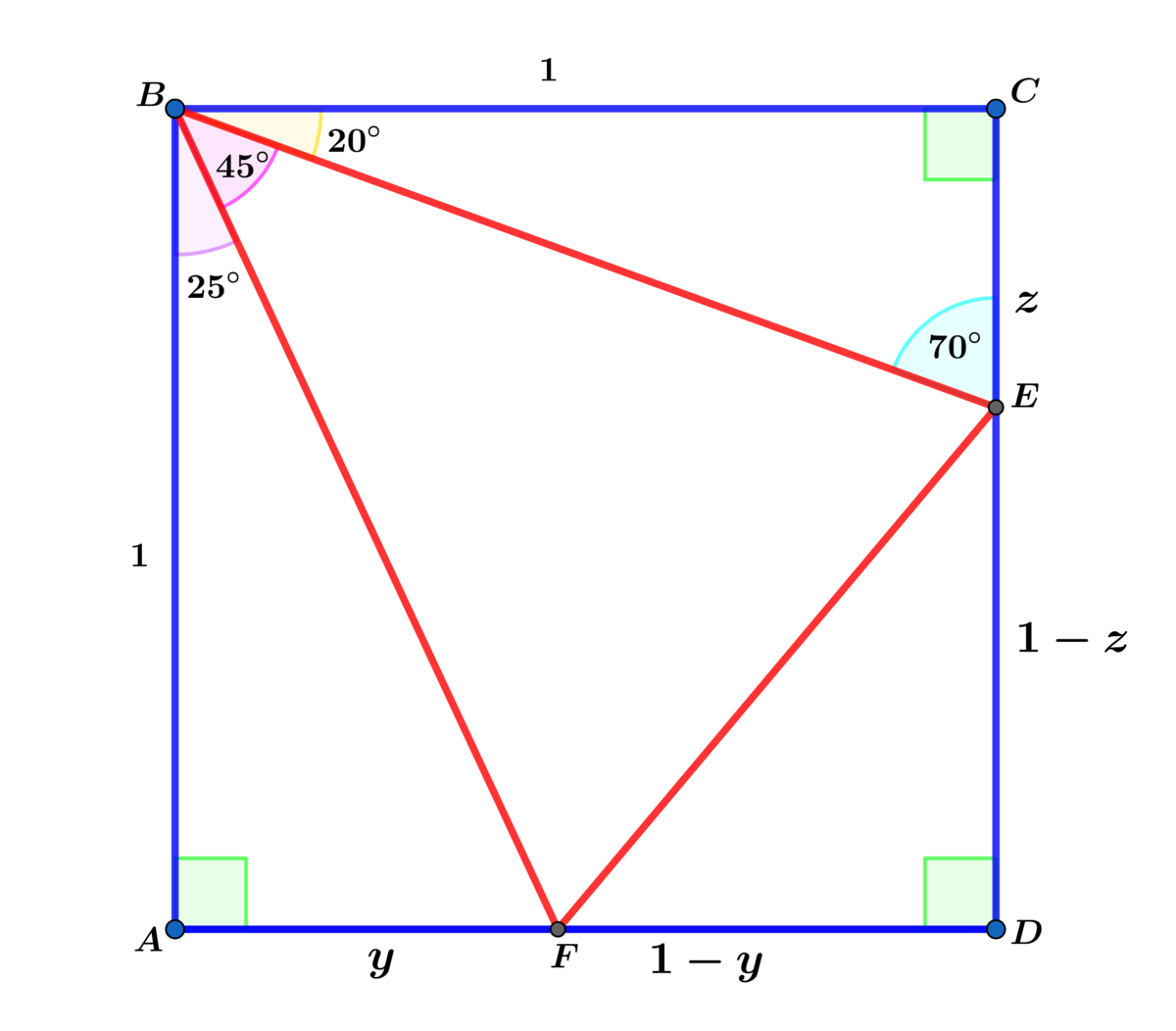
Using the diagram above y = tan ( 2 5 ∘ ) and z = tan ( 2 0 ∘ ) and
y = tan ( 2 5 ∘ ) = tan ( 4 5 ∘ − 2 0 ∘ ) = 1 + tan ( 2 0 ∘ ) 1 − tan ( 2 0 ∘ ) ⟹
F D = 1 − y = 1 + tan ( 2 0 ∘ ) 1 tan ( 2 0 ∘ ) and D E = 1 − tan ( 2 0 ∘ ) ⟹
F E = 1 + tan ( 2 0 ∘ ) 1 + tan 2 ( 2 0 ∘ ) ⟹
The perimeter P F E D = 1 + tan ( 2 0 ∘ ) 1 − tan 2 ( 2 0 ∘ ) + 2 tan ( 2 0 ∘ ) + 1 + tan 2 ( 2 0 ∘ ) =
1 + tan ( 2 0 ∘ ) 2 ( 1 + tan ( 2 0 ∘ ) ) = 2 .
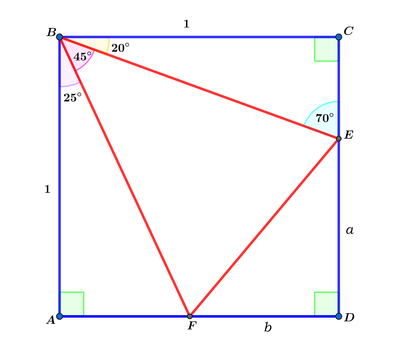
Let E D = a = 1 − tan 2 0 ∘ and F D = b = 1 − tan 2 5 ∘ . Then the perimeter is:
p = E D + F D + E F = E D + F D + E D 2 + F D 2 = a + b + a 2 + b 2 = 1 − tan 2 0 ∘ + 1 − tan 2 5 ∘ + ( 1 − t a n \2 0 ∘ ) 2 + ( 1 − tan 2 5 ∘ ) 2 = 1 − tan 2 0 ∘ + 1 − tan ( 4 5 ∘ − 2 0 ∘ ) + ( 1 − t a n 2 0 ∘ ) 2 + ( 1 − tan ( 4 5 ∘ − 2 0 ∘ ) ) 2 = 1 − t + 1 − 1 + t 1 − t + ( 1 − t ) 2 + ( 1 − 1 + t 1 − t ) 2 = 1 − t + 1 + t 2 t + ( 1 − t ) 2 + ( 1 + t 2 t ) 2 = 1 + t 1 − t 2 + 2 t + ( 1 + t ) 2 ( 1 − t ) 2 ( 1 + t ) 2 + 4 t 2 = 1 + t 1 + 2 t − t 2 + 1 + t ( 1 − t 2 ) 2 + 4 t 2 = 1 + t 1 + 2 t − t 2 + 1 + t t 4 + 2 t 2 + 1 = 1 + t 1 + 2 t − t 2 + t 2 + 1 = 1 + t 2 ( 1 + t ) = 2 Let t = tan 2 0 ∘
The remarkable thing here is that the perimeter is independent of ∠ C E B . As long as ∠ F B E = 4 5 ∘ , the perimeter of Δ D E F will always be 2 . Knowing that, I wonder if there's a simpler proof?
Log in to reply
I think my solution gives the answer, with ray B x dividing ∠ F B E in a way that ∠ E B x = ∠ E B C and ∠ F B x = ∠ F B A , which is always feasible.
Right angled triangles E B C and E B E ′ are congruent, thus B E ′ = B C = 1 ( 1 ) Similarly, if F ′ is the foot of the perpendicular from F on B x , triangles F B A and F B F ′ are congruent, thus B F ′ = B A = 1 ( 2 ) By ( 1 ) and ( 2 ) we conclude that B E ′ = B F ′ This means that points E ′ and F ′ coincide and thus E , E ′ , F ′ and F are collinear. Hence, B E ′ = B F ′ = B G .
So, we have two pairs of congruent triangles: △ B C E ≅ △ B G E and △ B A F ≅ △ B G F Consequently, C E = G E and F A = F G Now, we tackle the perimeter P of △ F E D : P = D F + F E + E D = D F + F G + G E + E D = D F + F A + C E + E D = D A + C D = 2