On bridges
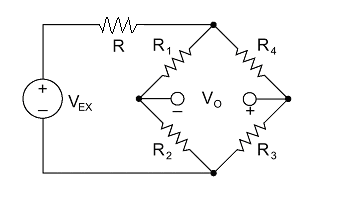 For the Wheatstone bridge above, let
R
=
1
3
3
9
1
Ω
,
R
2
=
2
5
2
Ω
,
R
4
=
1
2
0
Ω
,
V
E
X
=
5
V
dc. If
V
O
=
0
V
, and the voltage drop across
R
is
2
7
4
3
1
9
5
5
V
, determine the sum (in ohms) of the resistances
R
1
and
R
3
.
For the Wheatstone bridge above, let
R
=
1
3
3
9
1
Ω
,
R
2
=
2
5
2
Ω
,
R
4
=
1
2
0
Ω
,
V
E
X
=
5
V
dc. If
V
O
=
0
V
, and the voltage drop across
R
is
2
7
4
3
1
9
5
5
V
, determine the sum (in ohms) of the resistances
R
1
and
R
3
.
The answer is 356.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Using Excel, we can save from solving complicated equations.
140 Ω + 216 Ω = 356 Ω
Answer: 3 5 6
We first let the unknown values of the resistances as x and y .
Then, we note the relationship of resistors in a balanced Wheatstone bridge (we regard it as balanced when V O = 0 . That is,
R 1 ⋅ R 3 = R 2 ⋅ R 4
Simplifying, we get
x y = 3 0 2 4 0 .
This will be our first equation.
Now, by means of voltage divider theorem, and letting z be the total resistance of the bridge network, we can derive the following equation.
2 7 4 3 1 9 5 5 = 5 ⋅ 1 3 3 9 1 + z 1 3 3 9 1
2 7 4 3 1 9 5 5 = 3 9 1 + 1 3 z 1 9 5 5
It will be easy to determine that z = 1 3 2 3 5 2 .
Now, we get the values of x and y by simplifying the resistance network, and equating it to z . That is,
x + y + 3 7 2 ( x + 2 5 2 ) ( y + 1 2 0 ) = 1 3 2 3 5 2
Simplifying that, we get the equation x − 6 7 y + 1 1 2 = 0
Then, we integrate that with the first found equation, so we get the values
x = 1 4 0 Ω y = 2 1 6 Ω
So the answer is x + y = 3 5 6 Ω . Please don't forget to like/reshare!