On connection/Nash game
Consider a pair of planar dual (nodes of one lie in faces of another with intersecting edges) electrical networks, each with two terminal nodes. Here is an example in blue and red color:
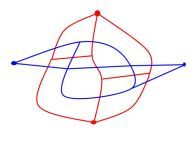Two players (blue and red) play a connection game taking turns choosing a new intersecting pair of edges, keeping their color's edge and deleting the opponent's edge. The goal is to connect the corresponding terminal nodes by a connected path of edges. Could the game end in a tie (both or none of the players connect)?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
At the end of the game after all choices were made, assign resistance tending to infinity to edges that were deleted and reciprocal resistance tending to zero for the eges that were left. Now, the effective resistance between terminal nodes will tend to zero if and only if there is a path berween them and to infinity if and only if the terminal nodes are disconnected. The product of the effective resistances is 1. Therefore, by continuity the effective resistances cannot both tend to zero or infinity, so one tends to zero and another to infinity and we have a winner with a path and a disconnected loser and the tie is impossible.