On Regular Polygons

As $n\to \infty$ , this polygon becomes closer to a circle. Therefore, $P$ and $A$ are the circumference and the area of a circle, respectively. Therefore, we have the answer as $\frac{2\pi r}{\pi r^2} = \frac{2}{r} = \frac{2}{2} = \boxed{1}.$

The $n$ sided polygon can be divided into $n$ isosceles triangles as shown in the figure:

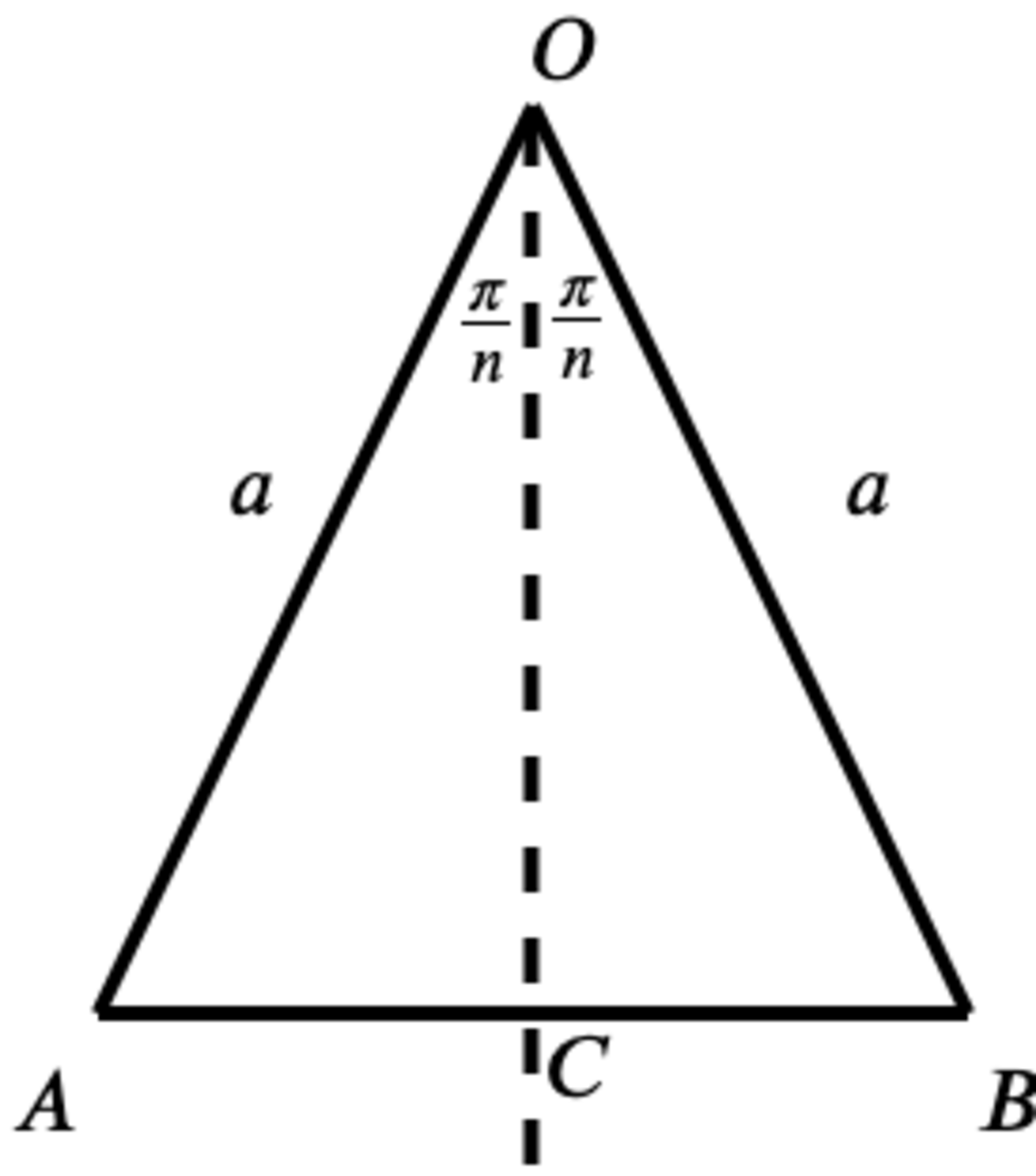
The base of the triangle can be found as such:

$AB = 2(AC) = 2(BC)=2a\sin\left(\frac{\pi}{n}\right)$

From here, the perimeter of the polygon can be found by multiplying $AB$ by $n$

$P = n(AB)= 2na\sin\left(\frac{\pi}{n}\right)$

The area of the isosceles triangle is:

$A_n = 2\left(\frac{1}{2}(OC)(AC)\right) = 2\left(\frac{1}{2}\left(a\sin\left(\frac{\pi}{n}\right)\right)\left(a\cos\left(\frac{\pi}{n}\right)\right)\right) = \frac{1}{2}a^2 \sin\left(\frac{2\pi}{n}\right)$

Area of the polygon is:

$A = nA_n$

After simplifying:

$\frac{P}{A} = \frac{2}{a\cos\left(\frac{\pi}{n}\right)}$

As $n$ becomes very large, the limit of $P/A$ becomes:

$\boxed{L = \frac{2}{a}}$

This solution describes a more rigorous approach. The interpretation that the polygon tends to a circle as $n$ becomes very large is correctly pointed out in other solutions.

$\begin{aligned} L&=\lim\limits_{n\rightarrow\infin}\frac{P}{A}\\ &=\frac{2πa}{πa^2}\\ &=\frac2a\\ &=\frac22\\ &=\boxed{1} \end{aligned}$

I am sorry I do not know how to draw so you people can either draw yourself or just imagine.
In order to calculate the area of any regular poygon with n number of sides let's divide it into n triangles by drawing lines from the centre of the plygon O to all the points of the polygon. Length of each of these lines is defined as a. Let's consider one of these triangles AOB with points A and B being the ends of any side of this polygon. This is an isocelese triangle. The angle AOB = 360 ÷ n. Let's draw a line from O to the point P which is centre of the line AB. Triangles AOP and BOP are equal and angle AOP = 360 ÷ 2n. Let's call it Y.
For triangle AOP AP = a × sinY and OP = a × cosY. Thus the area of triangle = a × sinY × a × cosY ÷ 2 and the area of triangle AOB = a × sinY × a × cosY.
Area of the whole polygon
a × sinY × a × cosY × n = A
We know AP = a × sinY thus AB = AP = a × sinY × 2 and the perimeter of the whole polygon is
a × sinY × 2 × n = P
Dividing A into P we get
a × cosY ÷ 2
We can see that as n gets bigger and bigger Y gets smaller and smaller thus for a circle with n as infinity Y is 0 and cos Y = 1 making the expression equal to a ÷ 2 which is exactly the ratio between the area and perimeter of any circle with a radius of a. I hop I have mathematically proven the circle to be the shape with maximum A to P ratio rather than just assuming it.

Actually its not smart or true way....any way i assume as n tends to infinity the polygon get closer and closer to circle shape and the ratio of perimeter of circle to its area is equal to 2/a.

na^2sin(180/n)cos(180/n) = A

2na(sin(180/n)) = P

(Lim [n↪inf] (A) = pia^2)

The area and perimeter get closer and closer to that of a circle with n increasing and converges to that of a circle in the limit.