On the Domino Ring
 Consider a set of
2
N
(
N
+
1
)
dominos which have faces of values 1 to N.
Consider a set of
2
N
(
N
+
1
)
dominos which have faces of values 1 to N.
A ring of dominos is a closed loop of them, in which any 2 touching dominos display the same value.
Let
F
(
N
)
be the minimum numbers of rings that are needed to use up all of these dominos.
Find the last three digits of n = 1 ∑ 2 0 1 6 F ( n ) .
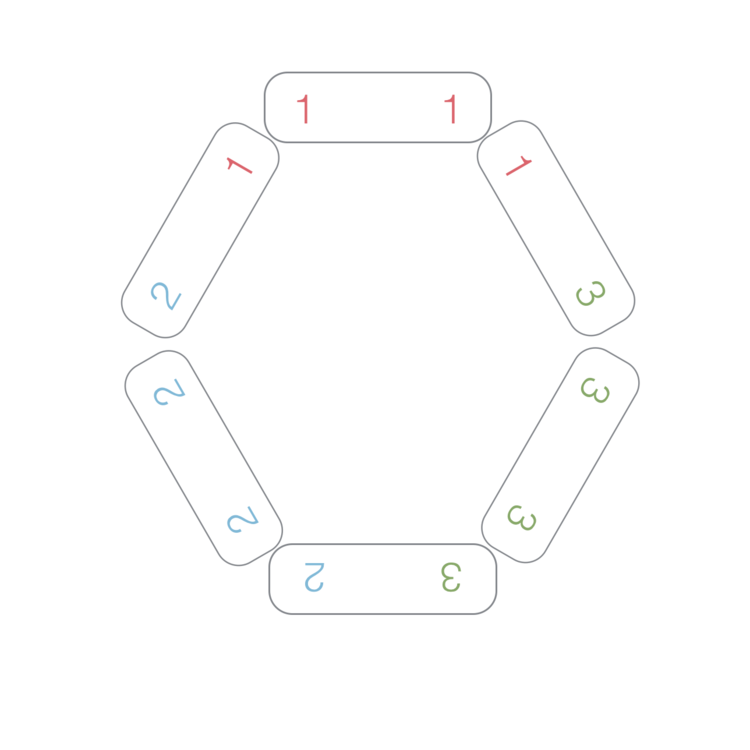
- As an explicit example, F ( 3 ) = 1 because we have the ring listed in the above image.
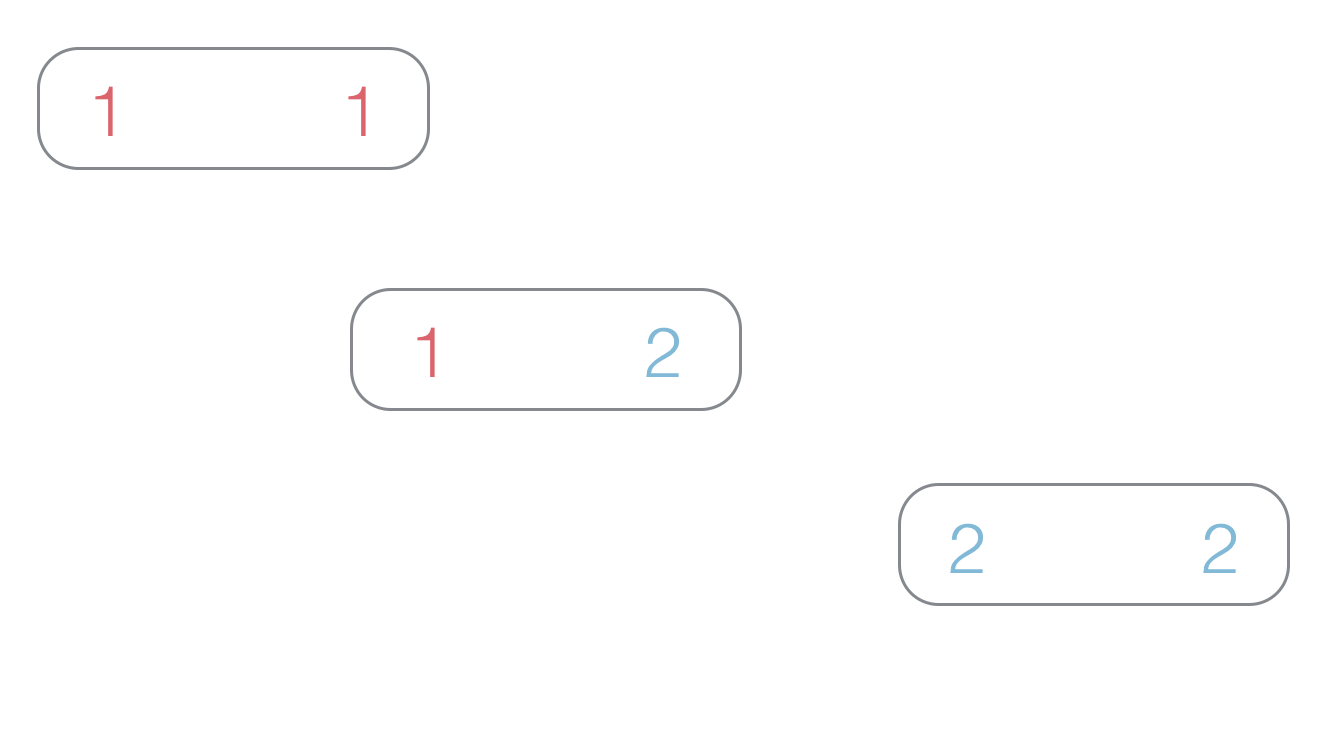
- For the purposes of this question, assume a single domino to be a ring. So F ( 2 ) = 3 (see image below) because there are three rings.
The answer is 553.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Moderator note:
Great solution!
It should be mentioned why N = 2 results in a different case than N = 2 k , which is because when the "alternate red edges" are removed, we end up with a disconnected graph (in which every vertex has an even number of edges). Whereas, for N ≥ 4 , we (have to verify) that we have a connected graph remaining.
Great problem! Got tricked by the n = 2 case at first, and answered 5 5 2 . Realized my mistake later.
Maybe I misunderstood the question but for a given N, aren't we supposed to have one domino for every distinct pair of number from 1 to N? You have the domino 1-1, 1-2, 1-3,...,1-n, 2-2,2-3,...,2-n, 3-3,...,3-n, ... n-n
Log in to reply
Yes. Your list is both of all the dominos and of all the edges in a complete graph. This is the key to the above solution.
I'm sorry but you did not proove that 1 + N/2 is the minimum. you simply showed one construction.
Log in to reply
If a number appears in a cycle of length greater than one, then it appears in pairs on adjacent dominos. This means that you will always take an even number of edges off a vertex in the complete graph to form these cycles. When N is even, the degree of each vertex is odd, hence leaving an odd number on each vertex when you can't form any more cycles. This means there are at least 2 N edges left over. Hence, 1 + 2 N is the minimum.
Consider N vertices labelled 1 , 2 , 3 , … N . Let the edge joining two vertices, say a and b represent the domino [ a ∣ b ] . Once we draw all the edges, we will obtain a complete graph along with a loop on each vertex.
In the problem, a ring is defined as either a single domino, which is a single edge on our graph, or it is defined as a closed loop, which is a Eulerian cycle on our graph. To use minimum number as rings, there should be more Eulerian cycles and of bigger size.
When N = 1 , the graph obtained is a single loop. It corresponds to a single domino [ 1 ∣ 1 ] . Therefore F ( 1 ) = 1 .
For all odd integers N , each vertex will be of even degree, and the graph is connected, so the entire graph is one Eulerian cycle; i.e. we can always find a path that starts and ends at the same vertex and uses each edge exactly once. Hence it is possible to use just one ring.
So, for all odd integers N , F ( N ) = 1 .
When N = 2 , the following graph is obtained.
There is no Eulerian cycle possible in this case, so we have to split it into three edges, so F ( 2 ) = 3 .
A connected graph is Eulerian iff each vertex has an even degree. If N is even, then each vertex has an odd degree. By separating out alternate edges on the perimeter of the polygon , we are left with a Eulerian graph.
For example N = 4 . We remove the alternate red edges of the square, and now each vertex has an even degree. It is now a Eulerian graph.
For even integers N ≥ 4 , F ( N ) = 1 + 2 N .
Therefore
n = 1 ∑ 2 0 1 6 F ( n ) = ( F ( 1 ) + F ( 3 ) + F ( 5 ) + … + F ( 2 0 1 5 ) ) + F ( 2 ) + ( F ( 4 ) + F ( 6 ) + … + F ( 2 0 1 6 ) = ( 1 0 0 8 × 1 ) + 3 + ( 1 0 0 7 × 1 + 2 4 + 2 6 + … + 2 2 0 1 6 ) = 1 0 0 8 + 3 + ( 1 0 0 7 + ( 2 + 3 + 4 + 5 + … + 1 0 0 8 ) ) = 1 0 1 1 + 1 0 0 7 + 2 1 0 0 8 × 1 0 0 9 − 1 = 2 0 1 8 + 5 0 4 × 1 0 0 9 − 1 ≡ 1 8 + 5 0 4 × 9 − 1 ( m o d 1 0 0 0 ) ≡ 1 8 + 4 5 3 6 − 1 ( m o d 1 0 0 0 ) ≡ 5 5 3 ( m o d 1 0 0 0 ) □
Please comment below if any step is not clear and I will explain it in detail.