Once Up, Twice Down
A point-mass (particle) is shot up an inclined plane that makes an angle θ with the ground. It slides up the incline to a certain distance, and then slides all the way back down. However, due to friction, the time it takes for the particle to slide from the maximum distance it reaches up the incline back to the bottom is twice the time it takes for it to go to the maximum distance up the incline from the bottom.
The coefficient of friction μ between the particle and the incline can be written as b a tan θ , where a and b are co-prime positive integers.
What is the value of a + b ?
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
@Milly Choochoo: Sorry, but I don't understand why you assumed the initial velocity for going up to be zero! > 2 a u t 2 = 2 a d ( 2 t ) 2 [ 'paragraph' and 'quote' formatting is not working :( ]
A small modification should make things clearer:
The displacement of the particle when it goes up the plane-
x u = v t − 2 1 a u t 2
Also, velocity after time ' t ' is zero.
v t = v − a u t
∴ 0 = v − a u t
∴ v = a u t
∴ v t = a u t 2
Plugging this back into the first equation, the solution can be justified.
x u = a u t 2 − 2 1 a u t 2
∴ x u = 2 1 a u t 2
Finally,
∣ x d ∣ = ∣ x u ∣
∴ 2 1 a u t 2 = 2 1 a d ( 2 t ) 2
Thanks! Nice quantitative response!
Here's the way I did it. The acceleration is -(gsinΘ+ugcosΘ) . The acceleration is -(gsinΘ-ugcosΘ)
Since the distance x you travel upwards is equal to the distance you travel downwards, and the time it takes to go down is twice the time it takes to go up, you can form two equations of motion.
UP: x = vt - (1/2)(gsinΘ+ugcosΘ)t^2
DOWN: x = (1/2)(gsinΘ-ugcosΘ)(2t)^2
Notice how in the down equation my acceleration is not negative. This is because I'm finding the distance traveled, not the displacement, so I use the magnitude of the acceleration.
Now set these equations equal to each other and after plugging in (3/5)tanΘ for u , you should get:
2v = gtsinΘ(5-3(a/b))
Now we can use the formula v=v_o+at. NOTE: THIS FORMULA ONLY APPLIES TO EQUATION OF MOTION GOING UP SINCE WHEN YOU GO DOWN, THE VELOCITY AT THE BOTTOM IS NOT EQUAL TO THE VELOCITY YOU LAUNCHED THE BLOCK AT DUE TO WORK DONE BY FRICTION
v=0 and v_0=v (our initial velocity). a = -(gsinΘ+ugcosΘ) .
So we have v = (gsinΘ+ugcosΘ)t . The negative in the acceleration gets canceled out when you subtract v on both sides.
Now you put the v equation above into the 2v = gtsinΘ(5-3(a/b)) .
After simplifying you should get 5a=3b. The only prime numbers that will satisfy this are a=3 and b=5. 3+5 = 8. They are the only prime numbers because when you look at a/b, you get a/b =3/5. 3/5 is in its simplest form and if you try to multiply it by any fraction equal to 1 (i.e. 5/5, 6/6), you will get a ratio that includes two nonprime numbers.
@Snehasish Karmakar, @Priyansh Saxena, and @Prateek Goyal, allow me to propose a different way of looking at this that might help you understand why the initial velocity and final velocity are irrelevant in this problem.
First off, what you are all saying is correct. The ball obviously starts off with an initial velocity, travels up the incline, and then arrives back down at the bottom of the incline with a different velocity.
What I would like to show you is that we can manipulate this hypothetical situation in such a way that we will not need to worry about the initial and final velocities.
For simplicity, I will call the acceleration of the ball when it is going up the incline a 1 , and the acceleration of the ball when it is going down the incline a 2 . I will also call the initial velocity of the ball V 0 , and the final velocity of the ball V f which is obviously less than V 0 because of the negative work done by friction.
Consider the initial problem - particularly the first part in which the ball is travelling up the incline. The ball is shot up the incline with a velocity V 0 , is subject to an acceleration a 1 , and travels up the incline a distance D .
Click to see a picture representation
Now what we can do is model the same situation, but in reverse.
If, hypothetically, the ball were to have been set at the final distance D up the incline and allowed to slide down the incline with the same acceleration a 1 (Which isn't actually possible, but bear with me), then at the bottom of the incline the ball will have traveled the same distance in the same amount of time T . The ball would have a velocity of V 0 at the bottom of the incline. This is just like saying a ball tossed vertically upwards will take an equal amount of time to travel up to a certain height as it will to travel back down that same height.
This concept lies in changing the acceleration from positive to negative.
Click to see what I'm talking about
Now we can model a displacement function for the point-mass particle that has the same acceleration a 1 , same solution for displacement D after time T , but with an initial velocity of zero.
D = 2 a 1 ( T 2 )
And if you were to integrate that with respect to time, you would see that the final velocity is equal to V 0 . Please note, this is obviously a different equation than the actual displacement function for the point-mass particle going up the incline. It just has a similar solution.
This equation is in the same V 0 = 0 form as the second part , when the point-mass particle is sliding down the incline.
D = 2 a 2 ( 2 T ) 2
We can now equate the two equations, cancel out the T 2 terms on each side, plug in the proper equations for a 1 and a 2 , and solve for μ , the coefficient of friction.
I do hope that this properly explained why I set the initial velocity to zero. If we were to set the initial velocity to a non-zero variable, then the acceleration would have to be negative .
We solve this problem by drawing F ree B ody D iagram(FBD) of both cases.
Resolving the forces acting on ball along and perpendicular to the incline, the FBD is--
 alt
alt
The forces are, the normal reaction( N ) and the downward force( mgsin θ ) due to weight of the ball AND the pseudo force( m a 1 & m a 2 ) in the direction of motion of ball(to account for dynamic equilibrium).
Now we just balance the resolved forces for both the cases--
FIRST CASE
Ball Going Up
1 N=mgcos θ
2 μ N+mgsin θ =m a 1
=> μ mgcos θ +mgsin θ =m a 1
=> a 1 = μ gcos θ +gsin θ
Using Laws of motion--
s=ut+ 2 1 a t 2
=> s= 2 1 a 1 T 2 --------- (1)
(because it is given that time taken to reach topmost position is 'T', so t=T & initial velocity u=0)
SECOND CASE
Ball Going Down
1 N=mgcos θ
2 μ N=mgsin θ +m a 2
=> a 2 = μ gcos θ -gsin θ
Again,
s=ut+ 2 1 a t 2
=> s= 2 1 a 2 ( 2 T ) 2 --------- (2)
(because it is given that time taken to reach bottommost position is '2T', so t=2T & initial velocity u=0)
Now, equating (1) and (2), we have--
2 1 a 1 T 2 = 2 1 a 2 ( 2 T ) 2
=> a 1 =4 a 2
=> μ gcos θ +gsin θ =4 μ gcos θ -4gsin θ
=>3 μ gcos θ =5gsin θ
=> μ = 3 5 tan θ
Hence,
5+3=8 ANS
:-)
You made a slight mistake in the second to last step there. You put
3 μ g cos θ = 5 g sin θ
When it was actually...
5 μ g cos θ = 3 g sin θ
Oh yes...thanks for pointing this out.
But the mistake is not in the second last step...actually I have messed up with the sign convention in eqn 2 FIRST CASE.
The correct eqn is " -( μ N+mgsin θ )=m a 1 "
Solve using this and everything else is correct and the answer is " μ = 5 3 tan θ "
I am really sorry for this guys... !
We can approximate the situation to have linear acceleration.
Clearly, the mass goes up until its velocity reaches zero and then falls. Since the time it takes to go up is half the time to go down, the average velocity to go up is twice the average velocity going down. Calculation the ratios of the average velocities(since it must be two), we have
v f = 2 v i
2 1 v f 2 = 8 1 v i 2
Clearly, we lost 3/4 of our kinetic energy. Since all lost energy is due to friction, letting l be the length up the slope the block goes up and down, the work done by friction is 3/4 of the initial KE:
8 3 v i 2 = ( μ k ) 2 g l cos θ (1)
Since 3/4 of the total kinetic energy was lost, in half the distance 3/8 of the initial mechanical energy was lost. Since at the peak of the slope all the mechanical energy is potential energy, and this is the 5/8 of the initial kinetic energy that was conserved,
1 6 5 v i 2 = g l sin θ (2)
Dividing (1) by (2) results in:
5 6 = 2 μ k cot θ
Simplifying,
5 3 tan θ = μ k
since i'm not much familiar with LaTex i ll name the angle of inclination as 'x' and coefficient of friction 'u' initial acceleration of the particle i.e while climbing the incline a 1 = gsinx+ugcosx final acceleration of the particle i.e. while descending the incline a 2 = gsinx -ugcosx Now, for both the journeys the particle covers equal distances therefore for any distance of the incline 'a' a = 1/2 a 1 t 2 = 1/2 a 2 t 2 4 plugging in the values we get the value of u = 3/5 tanx therefore ans = 8
forgive my opposite sign conventions
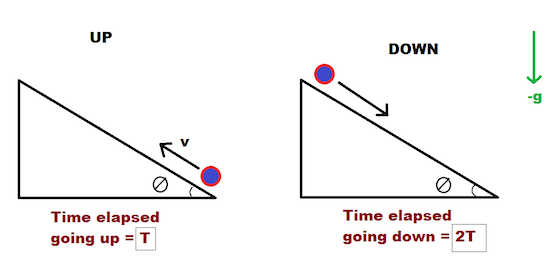
Let us make two situations called UP (when the particle is going up) and DOWN (when the particle is going down).
The accelerations due to the forces during UP and DOWN that are acting on the particle can be written as follows:
UP : − g sin θ − μ g cos θ
DOWN : − g sin θ + μ g cos θ
This can be easily seen by drawing a free-body diagram for both of the situations.
Now here's the important part. In both situations, they cover the same distance. However, in the DOWN situation, it took twice as long. Let a u represent the acceleration going up and a d represent the acceleration going down.
2 a u t 2 = 2 a d ( 2 t ) 2
2 a u t 2 = 4 × 2 a d t 2
a u = 4 a d
Now we just plug in our formulas for a u and a d that we wrote down earlier.
− g sin θ − μ g cos θ = 4 ( − g sin θ + μ g cos θ )
3 g sin θ = 5 μ g cos θ
μ = 5 3 tan θ
3 + 5 = 8