One COMPLEX integral(literally)

Note that the exponent is in the form $e^{ai}$ . So Euler's formula may help provided we can change the base into an appropriate form. But first, substituting $ln(u) = \tau$ and solving for $du$ , we get -

$I_{1}$ = $\displaystyle \int_{0}^{1} e^{\tau}(\tau - \tau^ {3}) d\tau$ = $\displaystyle \int_{1}^{e} (lnu - ln ^ {3} u) du$

Now, we see that the equation $lnu = ln ^ {3} u$ has solutions $u = 1,e$ . So this is just the area of the region bounded by the graphs of $lnu$ and $ln ^ {3} u$ .(Knowing that this is the case doesn't really help us, but it is a nice observation nonetheless). Applying integration by parts repeatedly gives us a value of $2e - 5$ .(Sorry I couldn't include this in the solution. It was just getting too long. You can solve this mini integral by using integration by parts repeatedly on $ln ^{3}(u)$ ).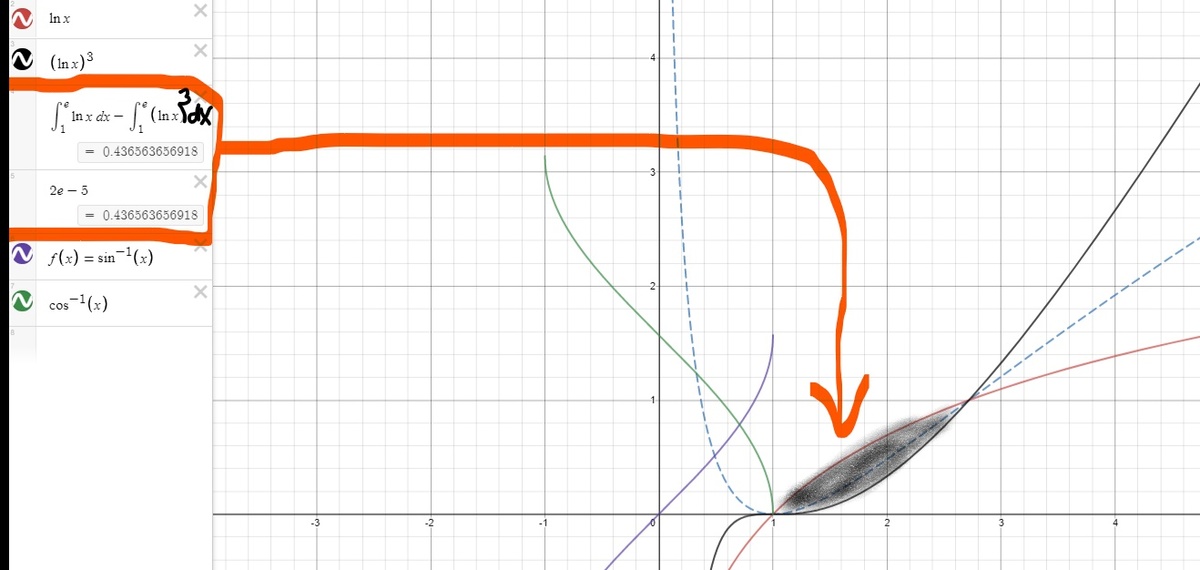

Adding $5$ and then multiplying by $\frac {1}{2}$ just gives us $e$ . So our integral simplifies to $i^ {-i}\displaystyle \int_{\frac {-\pi}{2}}^{\frac {\pi}{4}} e^{\sqrt [2i]{\frac {-2 + e^{ix} + e^{-ix}}{2i + ie^{ix} + ie^{-ix}}}} dx$

Factoring out a $-1$ and $i$ in the numerator and denominator respectively to simplify the exponent, and observing that $\frac {-1}{i} = i$ , we get -

$\sqrt [i] {\sqrt {\frac {i(1 -(\frac {e^{ix} + e^{-ix}}{2}))}{1 +(\frac {e^{ix} + e^{-ix}}{2})}}}$ = $(\sqrt{i} \cdot \sqrt {\frac {1 - \cos x}{1 + \cos x}}) ^{\frac {1}{i}}$ = $i^{\frac {-i}{2}} \cdot \tan (\frac {x}{2}) ^{-i}$ $\Rightarrow$ $I = i^ {-i}\displaystyle \int_{\frac {-\pi}{2}}^{\frac {\pi}{4}} e ^{(\sqrt{i} \cdot \tan (\frac {x}{2}))^ {-i}} dx$

(Here, we used the half-angle formulas for sine and cosine as well as the complex definition of cosine to turn this into a tangent).