One condition: No calculator!
If R = sin 1 3 0 ∘ + cos 1 3 0 ∘ , then which of the following is true?
Image Credit: Wikimedia Geek3 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Can you provide me a link where I can study all this ?
By the way, Neatly explained !!
You can visit the wiki of Trigonometry on Brilliant.
This is exactly how I did in my head! Nice job putting some actual math down!
We can use the identity sin θ + cos θ = 2 sin ( θ + 4 5 ∘ ) :
R = sin 1 3 0 ∘ + cos 1 3 0 ∘ = 2 sin ( 1 7 5 ∘ )
Since sin θ > 0 for 0 ∘ < θ < 1 8 0 ∘ , then R > 0 .
cos 1 3 0 ∘ = − cos 5 0 ∘ = − sin 4 0 ∘ sin 1 3 0 ∘ = sin 5 0 ∘ sin 5 0 ∘ > sin 4 0 ∘ ⇒ sin 5 0 ∘ − sin 4 0 ∘ > 0
We rewrite the terms as sin 5 0 − cos 5 0 . Now, c o s trails s i n in the domain ( 4 5 , 9 0 ) , where the numbers are expressed in degrees.
Hence, R > 0.
Just look at the graph provided, 1 3 0 o is slightly less than 4 3 π . At 4 3 π sum of the graph is 0. Slightly to its left, sum of the graph is > 0.
sin A + cos A is greater than zero if (0<A<135°) U (315°<A≤360°) and their respective coterminals. Since 130° < 135°, hence, R > 0.
Correction: A ≥ 0. Sorry i cannot edit it through my mobile phone.
sin130 + cos130 = sin50 - sin40 = 2sin5 × cos45 = √2 × sin 5 > 0.
This was the only solution that wouldn't have 2 answers
R = sin130° + cos130°
Squaring both sides gives you
R² = sin²130° + cos²130° + 2sin130°.cos130°
From trig identities,
sin²(∅) + cos²(∅) = 1, where ∅ is an angle.
2sin(∅).cos(∅) = sin(2∅), where ∅ is an angle.
By substituting this into the equation we have,
R² = 1 + sin(2×130°)
Further simplification
R² = 1 + sin(260°)
Since the angle 260° is in the third quadrant, we know that sin(260) is negative.
Also, since the angle 260° is greater than 180° and less than 270°, it means that sin(260°) is less than 0 (because sin180° = 0) but greater than -1 (because sin270° = -1)
Therefore,
R² = 1 - 0.xx (xx is any two digit number, we are ballparking here as we aren't allowed to use a calculator.)
R² = 0.xx
R = √(0.xx)
R = 0.xx
Therefore, R > 0.
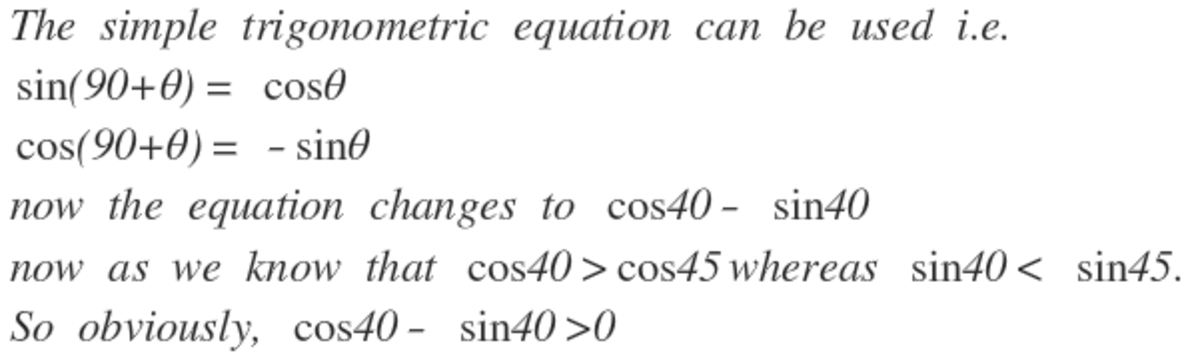
According to unit circle definition, cosine of an angle is represented on x-axis and sine of an angle is represented on y-axis.
Also,
sin 1 3 5 ° + cos 1 3 5 ° = 0
Which means that it is the mid point of circle.
Now from the circle it is evident that ∣ sin 1 3 0 ° ∣ > ∣ cos 1 3 0 ° ∣ and cos 1 3 0 ° is negative,
So,
Clearly sin 1 3 0 ° + cos 1 3 0 ° > 0