One crease - Two areas
Consider a sheet of paper, that has the shape of a unit square. Now fold the paper, so that the bottom right corner touches the centre of the upper edge:
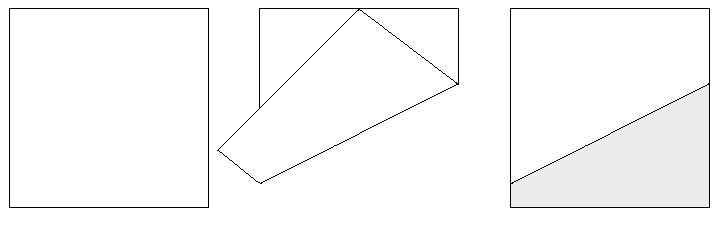
The crease divides the paper into two areas. What is the area of the grey shaded area?
The answer is 0.375.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
First lets draw some helpful triangles:
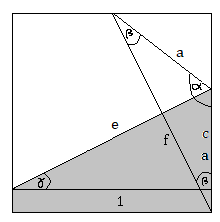
- e is our original crease.
- f is perpendicular to e and crosses the bottom right corner as well as the centre of the upper edge of the paper
- a is the length of the long parallel side of the grey trapezium
- c is one of the sides of the triangle with sidelengths: 1; f; c
The fact that we have two sides with sidelengths a can be explained by the folding process. If we drag the bottom right corner to the centre of the upper edge and then draw a line along our original side a we get another line with the sidelength a :
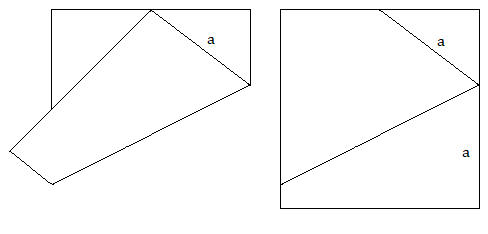
Because a shows up twice in the same triangle, we know that it is an isosceles triangle, so the angle β shows up twice aswell.
First up, we calculate the length of f with the pythagorean theorem: f = 1 2 + 0 . 5 2 = 1 . 1 1 8 0
Now let's have a look at this triangle:
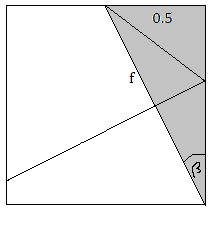
With the information give, we can calculate
β
, since
sin
β
=
f
0
.
5
β = arcsin ( f 0 . 5 ) = 2 6 . 5 6 5 °
Since all angles inside a triangle add up to 180° and since we know β shows up twice, we know the value of α :
α = 1 8 0 ° − 2 β = 1 2 6 . 8 7 0 °
Because e is perpendicular to the hypotenuse of this isosceles triangle, it cuts α and f exactly in half. We need to know that in order to calculate c , while looking at this triangle:
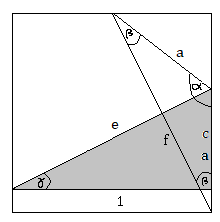
Again we can calculate the angle γ like before:
γ = 1 8 0 ° − 9 0 ° − 2 α = 2 6 . 5 6 5 ° = β
Now we can calculate c :
tan γ = 1 c = c = 0 . 5
Now let's name one last side:
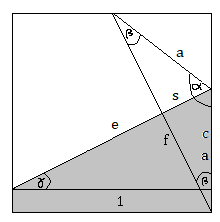
We can calculate that side s in the same manner we calculated c :
tan 2 α = 2 s f ……..-->………. s = tan 2 α f = 0 . 2 8 0 5
Now we can finally calculate a : a = s 2 + c 2 = 0 . 6 2 5
The last step is to calculate the area of our trapezium. We just need to add both parallel sides together, divide them by two and multiply them by the height of the trapezium (which is 1 in this case). The long parallel side is a with a = 0.625 . The short parallel side is just a − c . That gives us our final equasion: A = 2 a + ( a − c ) ∗ 1 = 0 . 3 7 5
Actually,this problem doesn't need to use trigonometry. Notice there are 2 pairs of congruent right triangle.
Log in to reply
I see that too now… Would have been a more elegant solution ;)
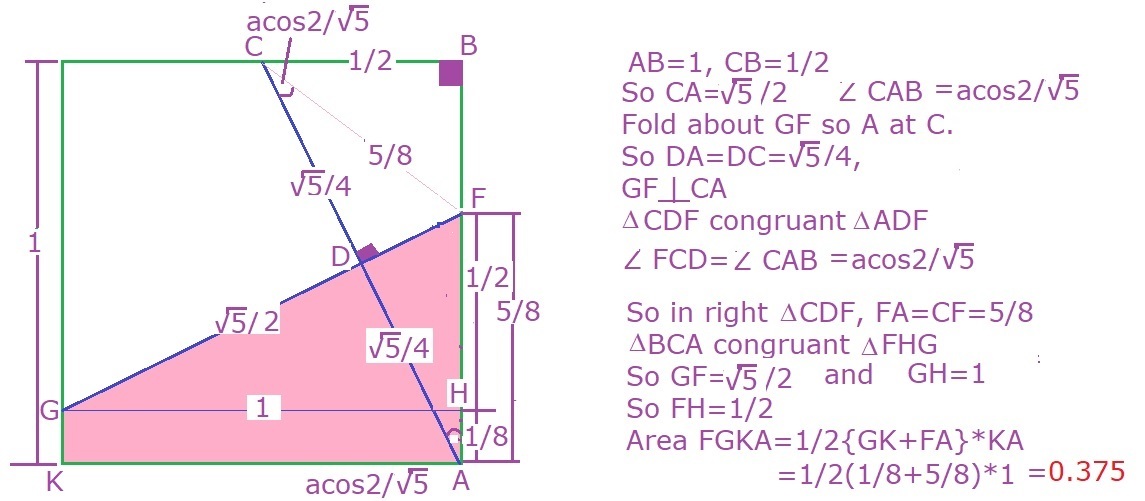
Draw an 8x8 grid on the square. The crease is the perpendicular bisector of the segment joining the bottom corner to the midpoint of the top edge. The segment as slope − 2 , so the crease has slope 2 1 and clearly hits the left and right sides as shown.
The grey region is a trapezoid with height 1 and bases 8 1 and 8 5
2 1 ∗ 1 ∗ ( 8 1 + 8 5 ) = 8 3 = 0 . 3 7 5