Infinite plus one cylinders
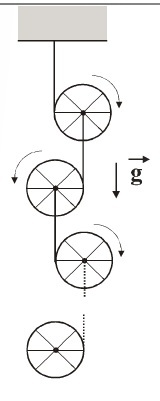 Find the acceleration of the first cylinder.
Find the acceleration of the first cylinder.
All have the same masses m and their moment of inertia is I = m r 2 .And the number of them goes to infinity. There is no slipping between the ropes and cylinders.
Answer as g a up to 3 decimal places.
If you like it share! Thanks!
The answer is 0.618.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This indeed a very beautiful problem. A recursion relation in a physics problem is pretty cool. Thanks a lot for sharing it :)
Oh nice although I could seen some recursions I didn't know how to proceed further but I just checked the ratios of T ( k ) / T ( k + 1 ) and found that they approached a limit of around 2.618.So I concluded that the Ratio of tensions in the 2 strings connecting the uppermost block must be 2 . 6 1 8 Then the ans came to be 0 . 6 1 8 ..Although one could try solving the recursion T ( n − 2 ) = 3 T ( n − 1 ) − T ( n ) .By setting some T ( n ) = γ ϕ n and using T ( n − 1 ) = 3 T ( n )
the 2nd equation, you mean a instead of v ?
My solution is not the most beautiful, (it uses a lot of algebra) but it only uses basic Newtonian equations of motion (no accelerated frames of reference and no energy equations).
The first idea is this: There will be some mass, M e f f which, when put in the place of the second pulley, will cause the first pulley to accelerate with the same acceleration as the infinite chain of pulleys caused.
The second idea is this: if you take the entire system and hang it from another pulley, the top pulley will behave in the same way as before (because the new system is identical).
These two ideas are illustrated by this drawing:
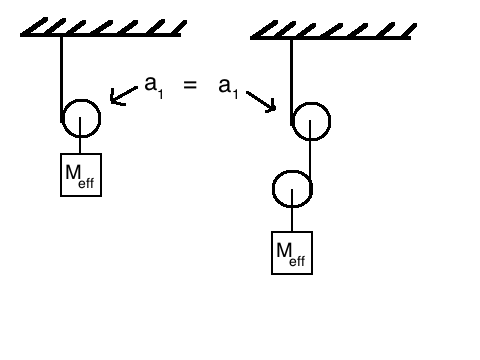
We can then solve the problem by describing the motion of both systems in my drawing, and then equating the accelerations of the top cylinders in both systems.
I have decided not to write the entire solution in detail, because I had to write 6 equations with 6 unknowns. Each equation was very simple (4 net force equations and 2 net torque equations) but it is a lot of algebra to eliminate all the variables.
Let's look at k-th cylindar and write these equations for him:
m a k = m g + T k + 1 − T k
α k R = v k − v k − 1
2 1 m v k 2 + 2 1 I ω k 2 = m g S k + T k + 1 S k − T k S k − 1
Combinateing these equations one can find relationship:
− a k − 1 + 3 a k − a k + 1 = g (1)
And here comes the best part.
We can suppose that a 1 has form like this a 1 = λ g .
And now if we go in the first cylindars frame of reference the effective gravity will be g ′ = g − a 1 and the second cylindar became first one and now his acceleration a 1 ′ = a 2 − a 1 = λ g ′ putting this in equation (1) you will get equation:
λ 2 + λ − 1 = 0
And the physical solution is :
λ = 2 5 − 1
I like this problem and hope you will too :)!