One-dimensional Photonic Crystal

Electricity and Magnetism Level 3

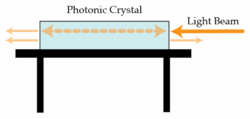Photonic crystals are materials which have dielectric constant which varies periodically, thus creating many interesting phenomena. One-dimensional photonic crystals are made from parallel layers with varying dielectric constants. We can analyze the unit cell of such crystals by examining the effect a single dielectric crystal has on a beam of light.

Suppose light enters the glass crystal in the image above from the right. Some percentage of the light will exit from the left and some from the right. The transmission coefficient at the air/glass interface is t = 0.7 t = 0.7 , and is the same in both directions. How much of the light in % exits the crystal on the left?


The answer is 53.85.

Andrzej Veitia by Andrzej Veitia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Vishal Sharma
Jan 31, 2014

Let the intensity of light entering from right be I .

But due to air-glass interface only 0.7 I will enter the crystal from right.

therefore 0.7 I will reach the other end (on the left side).

Again it will face an air-glass interface. therefore, 0.7 × 0.7 I 0.7 \times 0.7I will exit on the left and 0.3 × 0.7 I 0.3 \times 0.7I will rebound and travel towards the right side.

again upon reaching the right end (air-glass interface) 0.3 × ( 0.3 × 0.7 I ) 0.3 \times( 0.3\times 0.7I) will rebound and travel towards left.

this process repeats infinitely thus forming an infinite geometric progression whose first term will be 0.7 × 0.7 I 0.7 \times 0.7I and common ratio = 0.3 × 0.3 0.3 \times 0.3 = 0.09

thus summing the series will give:

0.7 × 0.7 I 1 − 0.09 \frac{0.7 \times 0.7I} {1-0.09}

= 0.5384 I

converting it to % gives 53.84% hence the answer..

9 Helpful 0 Interesting 1 Brilliant 0 Confused

There is an ambiguity to this problem I don't like. If one simply states the transmitted quantity one has no knowledge as to whether the incident field was partially absorbed or reflected. Therefore one cannot determine the internally reflected quantities without making certain assumptions which are by no means implicit for the given case.

Fanny Dufflager - 5 years, 6 months ago

I got the right answer but forget to convert it to %.

Chew-Seong Cheong - 7 years ago
Anish Puthuraya
Feb 2, 2014

This is a fairly easy problem.
Let the Strength of the light that enters the crystal from the right be E E .

Clearly,
Only 0.7 E 0.7E of light will enter it.

After reaching the other end,
only 0.3 × 0.7 E 0.3\times 0.7E of light will exit from the left.

This process occurs infinite times.

Thus, the total light that exits from the left is calculated as a Geometric Progression . The sum comes out to be,
0.539 E = 53.9 0.539E = \boxed{53.9} %

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...