One does not simply divide a circle.
Geometry
Level
pending
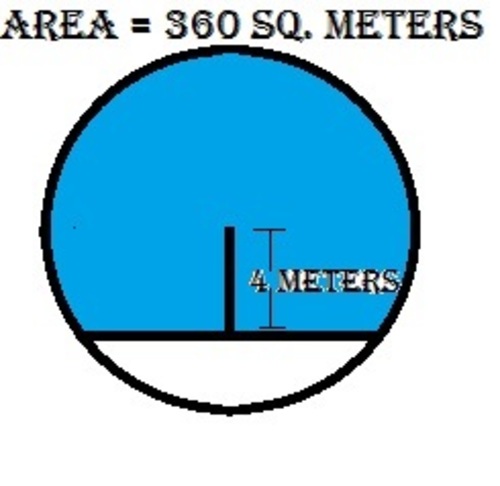A circle having an area of 360 square meters is divided into two segments by a chord which is 4 meters from the center of the circle. Compute the area of the larger segment. (Blue Portion = Larger Segment)
259.3745 sq. meters
276.4256 sq. meters
263.6011 sq. meters
289.5546 sq. meters
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Area of Circle = 360 square meters
Distance from center to chord = 4 meters
Area of Circle = (pi)(r^2)
r=sq.rt (area/pi)
r=sq.rt(360 sq. meters/pi)
r=10.7047447 meters
Half of chordal length = sq.rt [(r^2)-(4 meters)^2]
Half of chordal length = 9.929328226 meters
Chordal length = 19.85865645 meters
Area of Triangle =(1/2)(Chordal length)(4 meters)
Area of Triangle = 39.71731291 sq. meters
Half of Vertex Angle = arccos (4/r)
Half of Vertex Angle = 68 degrees 3 minutes 29.19 seconds
Vertex Angle = 136 degrees 6 minutes 58.37 seconds
Vertex Angle = 2.375676118 radians
Sector Area = (1/2)(2.375676118 radians)(r^2)
Sector Area = 136.1162151 sq. meters
Area of Smaller Segment = Sector Area - Triangle Area
Area of Smaller Segment = 136.1162151 sq. meters - 39.71731291 sq. meters
Area of Smaller Segment = 96.39890223 sq. meters
Area of Larger Segment = Area of Circle - Area of Smaller Segment
Area of Larger Segment = 360 sq. meters - 96.39890223 sq. meters
Area of Larger Segment = 263.6010978 sq. meters
Final Answer: 263.6011 sq. meters