One Half is Green
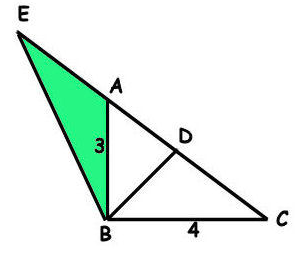 is a triangle,
is the bisector of angle
,
is extended to
with
. Find the measure of
so that the area of
is half the area of
. Give your answer to 3 decimal places.
is a triangle,
is the bisector of angle
,
is extended to
with
. Find the measure of
so that the area of
is half the area of
. Give your answer to 3 decimal places.
The answer is 50.206.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
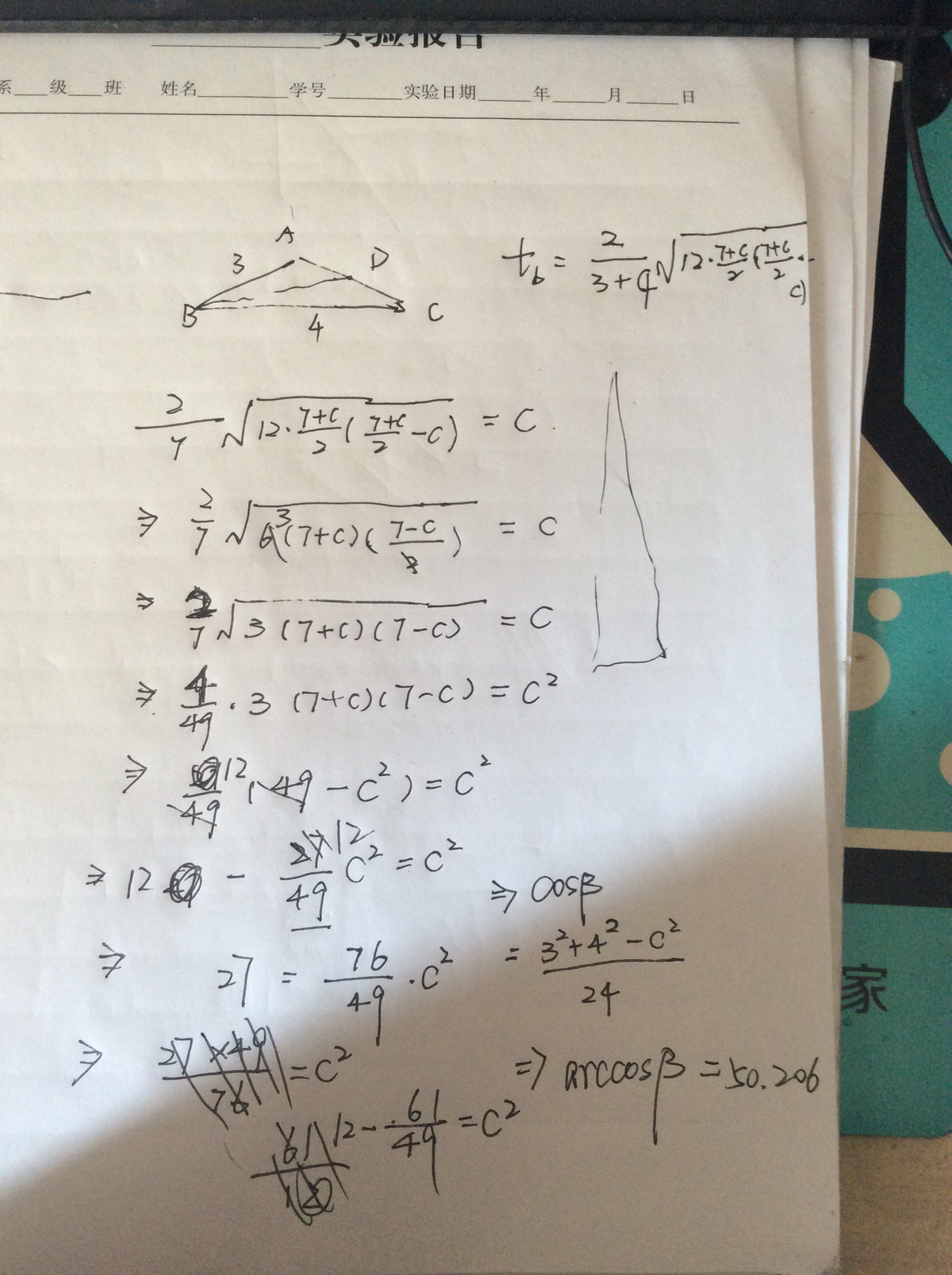
In order to have the areas of Δ E A B and Δ A B C the same we will require that ∣ A E ∣ = ∣ A C ∣ , since the two triangles share the same altitude to E C . But since we require that ∣ A E ∣ = ∣ B D ∣ we have that ∣ B D ∣ = ∣ A C ∣ .
Now the bisector length formula gives us that
∣ B D ∣ 2 = ( 4 + 3 ) 2 4 ∗ 3 ( ( 4 + 3 ) 2 − ∣ A C ∣ 2 ) ,
which after substituting ∣ A C ∣ = ∣ B D ∣ and simplifying yields that
4 9 ∗ ∣ A C ∣ 2 = 1 2 ( 4 9 − ∣ A C ∣ 2 ) ⟹ ∣ A C ∣ 2 = 6 1 5 8 8 .
Now by the Cosine rule we have that
∣ A C ∣ 2 = ∣ A B ∣ 2 + ∣ B C ∣ 2 − 2 ∣ A B ∣ ∣ B C ∣ cos ( ∠ B )
⟹ 6 1 5 8 8 = 9 + 1 6 − 2 4 cos ( ∠ B )
⟹ cos ( ∠ B ) = 1 4 6 4 9 3 7 ⟹ ∠ B = arccos ( 1 4 6 4 9 3 7 ) = 5 0 . 2 0 6 ∘ to 3 decimal places.