One Large Triangle
If ∠ C = 1 2 0 ° and sides a , b , and c are integers such that a < b < c , g cd ( a , b , c ) = 1 , and a + 2 b − 2 c a − b − 2 c = 1 5 0 0 , then find the perimeter of △ A B C .
The answer is 4504501.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I bet there's a better way to do this - the form of that square root is pretty unusual!
Log in to reply
There might be, but I did it pretty much the same way that you did!
Can you prove that the following setup too?
If 0 < a < b < c are coprime integers such that a 2 + b 2 + a b = c 2 and a + 2 b − 2 c a − b − 2 c = 1 5 0 0 , then a + b + c = 3 0 0 1 + 2 2 4 9 9 9 9 9 + 2 2 5 1 5 0 1 = 4 5 0 4 5 0 1 .
That is, this time, we do not know that a , b , c are side lengths of a triangle.
Update: Wait, this is silly. a 2 + b 2 + a b = c 2 implies that we can form a triangle with ∠ C = 1 2 0 ∘ . I'm sorry for wasting your time.
Log in to reply
Ha, not at all - you'd already edited by the time I saw this. But it's interesting to think what the condition a + 2 b − 2 c a − b − 2 c = k actually means. I've tried fixing points A and B and looking at the locus of valid points C , but I don't recognise the shape of it:
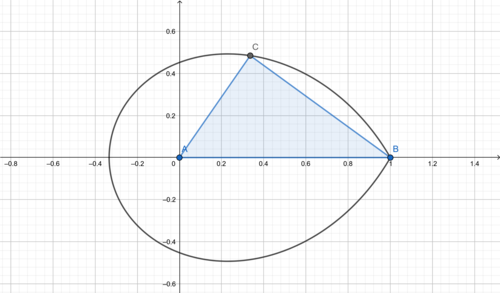
A pointy egg? Not very mathematical...(actually, it looks a bit like half a lemniscate to me, but I don't know why that would be)
Since the diameter of the circumcircle of △ A B C , D = sin A a = sin B b = sin C c , then
a + 2 b − 2 c a − b − 2 c sin A + 2 sin B − 2 sin C sin A − sin B − 2 sin C sin A + 2 sin ( 6 0 ∘ − A ) − 2 sin 1 2 0 ∘ sin A − sin ( 6 0 ∘ − A ) − 2 sin 1 2 0 ∘ 2 cos A − 2 3 sin A − cos A − 2 6 t 2 3 − 2 3 t + t 2 2 t 3 − t ⟹ t = 1 5 0 0 = 1 5 0 0 = 1 5 0 0 = 1 5 0 0 = 1 5 0 0 = 1 5 0 0 = 3 0 0 1 3 Let t = tan 2 A Since A < 6 0 ∘
Then we have:
a : b : c = sin A : sin ( 6 0 ∘ − A ) : sin 1 2 0 ∘ = 1 + t 2 2 t : 2 ( 1 + t 2 ) 3 ( 1 − t 2 ) − 2 t : 2 3 = 4 t : 3 ( 1 − t 2 ) − 2 t : 3 ( 1 + t 2 ) = 3 0 0 1 4 : 1 − 3 0 0 1 2 3 − 3 0 0 1 2 : 1 + 3 0 0 1 2 3 = 1 2 0 0 4 : 8 9 9 9 9 9 6 : 9 0 0 6 0 0 4 = 3 0 0 1 : 2 2 4 9 9 9 9 : 2 2 5 1 5 0 1
Therefore a + b + c = 3 0 0 1 + 2 2 4 9 9 9 9 + 2 2 5 1 5 0 1 = 4 5 0 4 5 0 1 .
Nice creative solution!
Just like Euclid's formula for Pythagorean triples, there is a formula to generate integer triangles with an angle of 1 2 0 ∘ ; if n < m are integers, then the triangles with sides 2 m n + n 2 , m 2 − n 2 , m 2 + m n + n 2 has an angle of 1 2 0 ∘ opposite the longest side. To ensure the sides are coprime, we need g cd ( m , n ) = 1 and also m − n cannot be a multiple of 3 .
There are two ways to assign the shorter sides, so two cases to check. For neatness, write k = 1 5 0 0 :
Case a = 2 m n + n 2 , b = m 2 − n 2 , c = m 2 + m n + n 2 :
a + 2 b − 2 c a − b − 2 c = 2 m n + n 2 + 2 m 2 − 2 n 2 − 2 m 2 − 2 m n − 2 n 2 2 m n + n 2 − m 2 + n 2 − 2 m 2 − 2 m n − 2 n 2 = − 3 n 2 − 3 m 2 = n 2 m 2
so that m = k n . The only coprime pair satisfying this is ( m , n ) = ( 1 , k ) giving sides a = 2 k + 1 , b = k 2 − 1 , c = k 2 + k + 1 and perimeter P = 2 k 2 + 3 k + 1 = ( k + 1 ) ( 2 k + 1 ) . In this case, the perimeter is P = 1 5 0 1 × 3 0 0 1 = 4 5 0 4 5 0 1 .
Case a = m 2 − n 2 , b = 2 m n + n 2 , c = m 2 + m n + n 2 :
Switching the values of a and b , a + 2 b − 2 c a − b − 2 c = m 2 − n 2 + 4 m n + 2 n 2 − 2 m 2 − 2 m n − 2 n 2 m 2 − n 2 − 2 m n − n 2 − 2 m 2 − 2 m n − 2 n 2 = − m 2 + 2 m n − n 2 − m 2 − 4 m n − 4 n 2 = ( m − n ) 2 ( m + 2 n ) 2
so now we need m + 2 n = k ( m − n ) . Rearranging, this leads to ( k − 1 ) m = ( k + 2 ) n
In this case, g cd ( k − 1 , k + 2 ) = 1 so the only coprime pair that works is ( m , n ) = ( 1 5 0 2 , 1 4 9 9 . But these don't satisfy the condition that m − n isn't a multiple of 3 , so the sides a , b , c in this case are not coprime. In fact, this triangle is just a scaled version of the one found in the first case.
So the unique answer is P = 4 5 0 4 5 0 1 .