Stanley's Saga

Probability Level 3

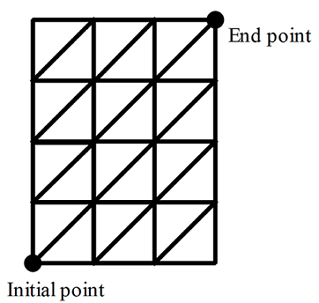
The protagonist of this story, Stanley, is standing peacefully at coordinates $(0, \space 0)$ without any concern in his life whatsoever.

Now, Stanley will move at coordinates $(3, \space 4)$ .

If Stanley only goes either up, or right, or up-right (corresponding vectors in their respective order: $\vec{u}(0, \space 1)$ , $\vec{r}(1, \space 0)$ , $\vec{ur}(1, \space 1)$ ), on how many ways can Stanley accomplish this tremendous stunt?

The answer is 129.

3 solutions

Kai Ott
Jun 30, 2016

Relevant wiki: Rectangular Grid Walk

Consider the number of moves he takes to get to the point (3/4). That depends on the number of times he takes the vector (1/1). There are four cases.

Case 1: $4×u + 3×r +0×ur \to {7 \choose 4} \cdot {3 \choose 3} = 35$ possibilities.

Case 2: $3×u + 2×r +1×ur \to {6 \choose 3} \cdot {3 \choose 2} = 60$ possibilities.

Case 3: $2×u + 1×r +2×ur \to {5 \choose 2} \cdot {3 \choose 1} = 30$ possibilities.

Case 4: $1×u + 0×r +3×ur \to {4 \choose 1} \cdot {3 \choose 0} = 4$ possibilities.

Hence the total number of possibilities is $35 + 60 + 30 + 4 = 129.$

Manuel Kahayon
Jun 28, 2016

Relevant wiki: Rectangular Grid Walk

Milan-kun, I think you need to specify that he needs to go to exactly one of either of the points.

Well, anyways, I've used the standard "Sum off the number of ways to get to each vertex procedure", as follows:

P.S. Stanley's parables?

Milan-kun!? I feel like some anime character (which is good to some extent). I don't mind using suffixes. :3

I am not certain whether I should specify that it is completely indifferent whether he gets at (3, 4) or at (4, 3), but if someone is having a doubt concerned that specifically, then I believe that will be asked in the provided FAQs. Did you solve the problem on your first guess? (meaning: did the "(3,4) or (4,3)" affected your answers)

And the P.S. Yes, at the moment of making this problem, narrator's voice from Stanley's parable was in my mind, so I shall say that I recreated the humor of it (to some degree).

And one more thing from me. Is your "avatar picture" (profile pic) from some anime? If yes, do you mind telling me which one.

Milan Milanic - 4 years, 11 months ago

Hmm... I don't quite remember myself... As far as I know a teammate of mine showed me the pic and I decided to download it, and searching for it resulted in the visual novel Gensou no Idea.

Manuel Kahayon - 4 years, 11 months ago

I just went for the what you wrote, that he goes to (3/4) and didn't care for the picture with the twi possible end points. Because if he can go to either of the two points, then the answer would be 129×2=258.

Kai Ott - 4 years, 11 months ago

Ali Qureshi
Jul 2, 2016

Let us consider four separate cases.

case#1

When there are no transverse moves, then there are 3 horizontal moves and 4 vertical moves like r,r,r,u,u,u,u. And all such moves are

$\frac{7!}{3! \times 4!} = 35$

case#2

When there is 1 transverse move, then there will be 2 horizontal and 3 vertical moves like r,r,(ru),u,u,u. All such moves are

$\frac{6!}{2! \times 3!} = 60$

case#3

When there are 2 transverse move, then there will be 1 horizontal and 2 vertical moves like r,(ru),(ru),u,u. All such moves are

$\frac{5!}{2! \times 2!} = 30$

case#4

When there are 3 transverse move, then there will be no horizontal move and just 1 vertical moves like (ru),(ru),(ru),u. All such moves are

$\frac{4!}{3! \times 1!} = 4$

Therefore, all possilble moves to reach (3,4) from (0,0) under the given conditions are 35 + 60 + 30 + 4 = 129

Stanley's Saga

The answer is 129.

3 solutions

0 pending reports