One Odd Octadecagon
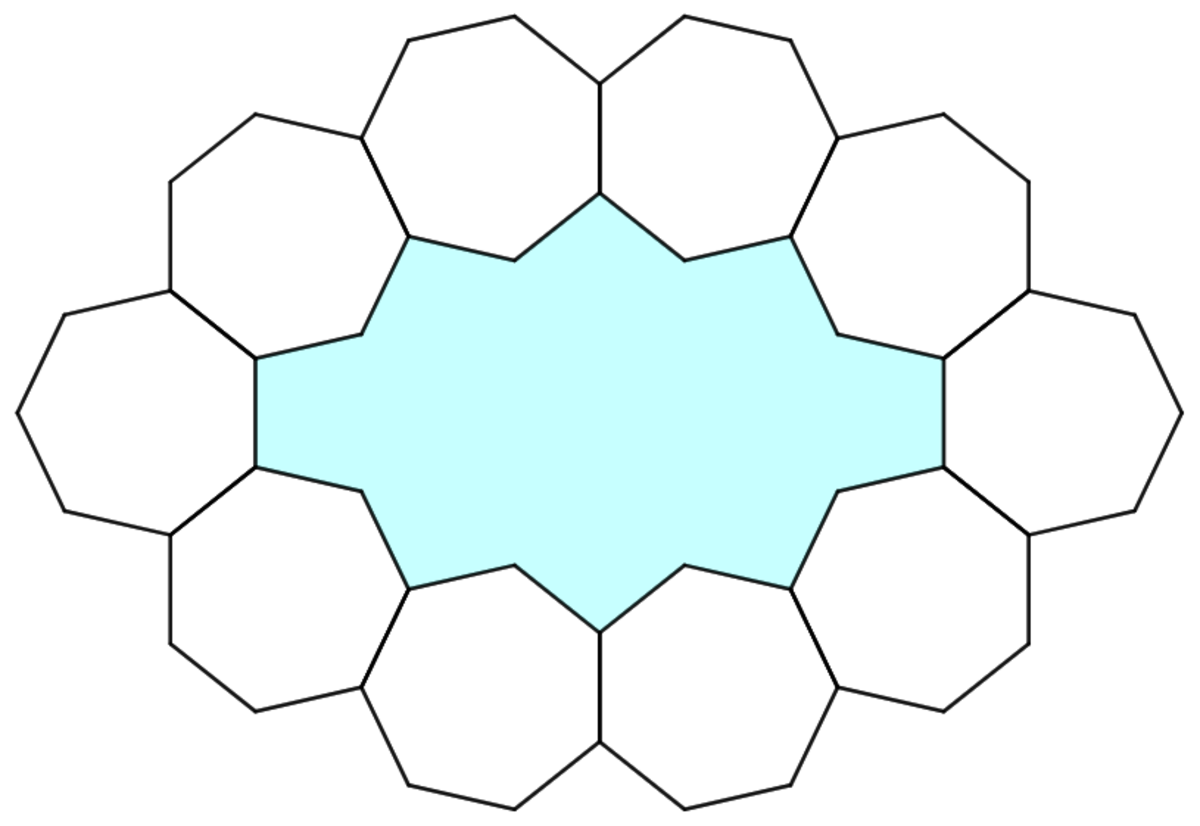
As shown above, the cyan polygon is surrounded by 10 unit regular heptagons. If the area of the cyan polygon can be expressed as
A sin 7 π + B sin 7 2 π + C sin 7 3 π
where A , B , and C are integers. Input the product A B C as your answer.
The answer is 198.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The cyan polygon can be tiled with 6 purple unit rhombi (with interior angles of 7 π and 7 6 π ), 3 green unit rhombi (with interior angles of 7 2 π and 7 5 π ), and 1 1 blue unit rhombi (with interior angles of 7 3 π and 7 4 π ), as follows:
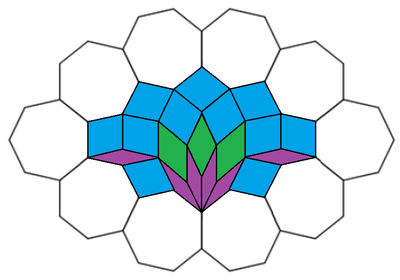
Since each purple unit rhombi has an area of 2 ⋅ 2 1 ⋅ 1 ⋅ 1 ⋅ sin 7 π = sin 7 π , each green unit rhombi has an area of 2 ⋅ 2 1 ⋅ 1 ⋅ 1 ⋅ sin 7 2 π = sin 7 2 π , and each blue unit rhombi has an area of 2 ⋅ 2 1 ⋅ 1 ⋅ 1 ⋅ sin 7 3 π = sin 7 3 π , the total area is:
6 sin 7 π + 3 sin 7 2 π + 1 1 sin 7 3 π .
Therefore, A = 6 , B = 3 , C = 1 1 , and A B C = 1 9 8 .
Wow! Neatest solution so far! Nice!
Log in to reply
Scintillating question, Michael!!!!!
I was pretty pleased when I found this tiling solution! Great question!
Simply brilliant! You left me speechless @David Vreken ! This is a proof that math is indeed beautiful!
Note that we can cut the shape into smaller regions area as shown below where congruent shapes are colored alike. Also note that the internal angle of a regular heptagon is θ = 7 5 π , which can be easily derived if we draw segments from the center of the heptagon to each vertex and find the angles of one of the resulting seven congruent isosceles triangles. The identities sin ( π − x ) = sin ( x ) , sin x . sin y = 2 cos ( x − y ) − cos ( x + y ) , cos x . cos y = 2 cos ( x − y ) + cos x + y and sin x . cos y = 2 sin ( x − y ) + sin ( x + y ) will be used a lot in the course of our work so whenever the first one is used, it will be colored in blue, and whenever one of the other three is used, it will be colored in green. Sometimes the green formulae will be used for x = y and will be equivalent to 2 sin x cos x = sin 2 x , 2 sin 2 x = 1 − cos 2 x and 2 cos 2 x = cos 2 x + 1 .
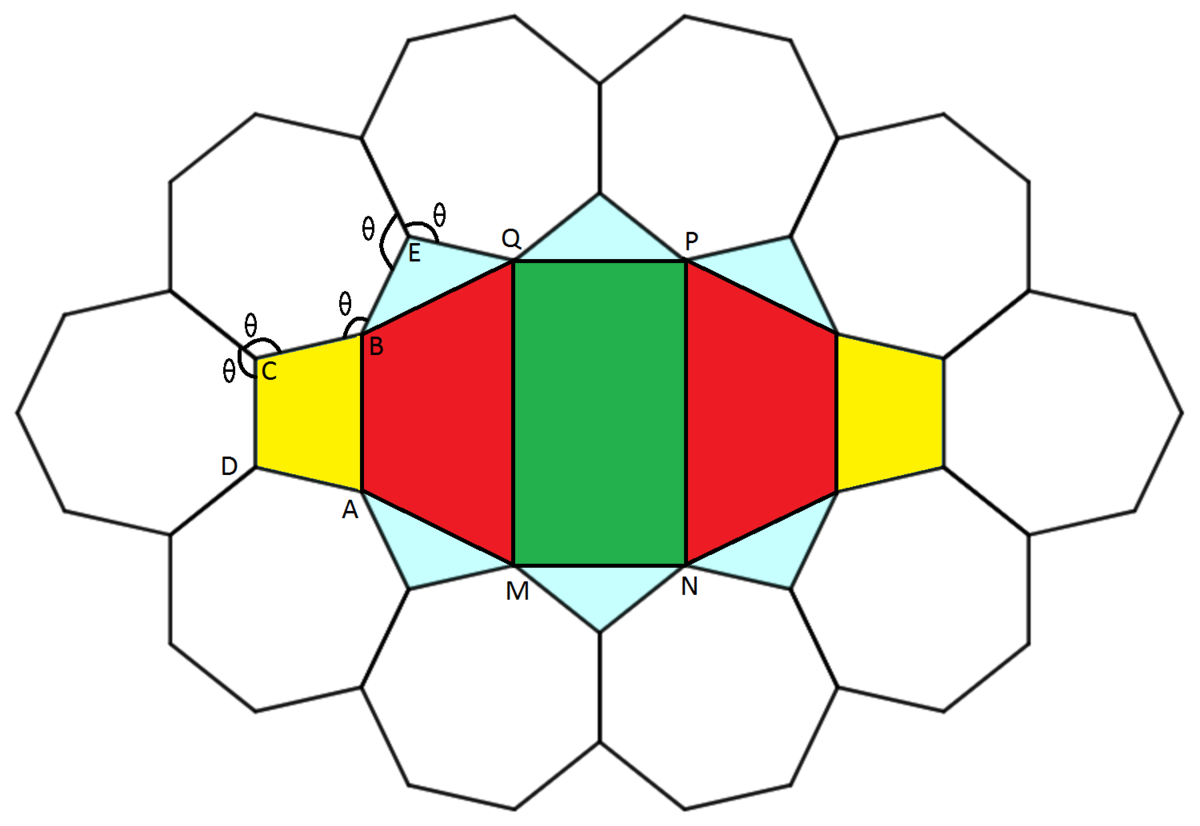
We'll address each of the four shapes individually. 1 . Cyan Triangle ( △ B E Q ) .
It is an isosceles triangle with equal side-lengths of 1 and ∠ E = 2 π − 2 θ = 7 4 π . Also ∠ B = ∠ Q = 1 4 3 π . Its area is: S cyan = 2 B E . E Q . sin ∠ B E Q = 2 sin 7 4 π = 2 sin 7 3 π Drawing the height from ∠ E we get two congruent right triangles with which it's easily found that B Q = 2 sin 7 2 π = Q P since these two segments are bases of the congruent triangles. 2 . Yellow Trapezoid ( A B C D ) .
It is an isosceles trapezoid. Draw the heights from C and D to the base and label the intersection points with C 1 and D 1 . The two heights split the trapezoid to two congruent right triangles and a rectangle. ∠ C = 2 π − 2 θ = 7 4 π ⇒ ∠ B = 7 3 π . Then: A D 1 = B C 1 = cos 7 3 π ; C C 1 = h = sin 7 3 π ; A B = A D 1 + D 1 C 1 + C 1 B = 2 cos 7 3 π + 1 S yellow = 2 ( A B + C D ) h = sin 7 3 π cos 7 3 π + sin 7 3 π = 2 sin 7 6 π + sin 7 3 π = 2 sin 7 π + sin 7 3 π 3 . Red Trapezoid ( M Q B A ) .
It is again an isosceles trapezoid but its legs are A M = B Q = 2 sin 7 2 π (which we know from above). Again, draw the heights A A 1 and B B 1 and split the trapezoid to a rectangle and and two congruent right triangles. First: ∠ Q B A = 2 π − ( ∠ A B C + θ + ∠ Q B E ) = 1 4 9 π ⇒ ∠ M Q B = 1 4 5 π Now from △ B B 1 Q ≅ △ A A 1 M we have: M A 1 = Q B 1 = B Q cos 1 4 5 π = 2 sin 7 2 π cos 1 4 5 π cos ( 2 π − x ) = sin x M A 1 = Q B 1 = 2 sin 7 2 π sin 7 π B B 1 = h 1 = B Q sin 1 4 5 π = 2 sin 7 2 π sin 1 4 5 π sin ( 2 π − x ) = cos x B B 1 = h 1 = 2 sin 7 2 π cos 7 π M Q = M A 1 + A 1 B 1 + B 1 Q = 2 M A 1 + A B = 4 sin 7 2 π sin 7 π + 2 cos 7 3 π + 1 Using the formula for trapezoid's area: S red = 2 ( M Q + A B ) h 1 = ( 4 sin 7 2 π sin 7 π + 4 cos 7 3 π + 2 ) sin 7 2 π cos 7 π S red = 2 sin 2 7 2 π . 2 sin 7 π cos 7 π + 2 sin 7 2 π ( 2 cos 7 π cos 7 3 π ) + 2 sin 7 2 π cos 7 π S red = ( 1 − cos 7 4 π ) sin 7 2 π + 2 sin 7 2 π cos 7 2 π + 2 sin 7 2 π cos 7 4 π + sin 7 π + sin 7 3 π S red = sin 7 2 π − sin 7 2 π cos 7 4 π + sin 7 4 π + sin 7 − 2 π + sin 7 6 π + sin 7 π + sin 7 3 π S red = sin 7 2 π − 2 1 sin 7 − 2 π − 2 1 sin 7 6 π + sin 7 3 π − sin 7 2 π + sin 7 π + sin 7 π + sin 7 3 π S red = sin 7 2 π + 2 1 sin 7 2 π − 2 1 sin 7 π + sin 7 3 π − sin 7 2 π + sin 7 π + sin 7 π + sin 7 3 π Collecting like terms results in: S red = 2 3 sin 7 π + 2 1 sin 7 2 π + 2 sin 7 3 π 4 . Green Rectangle ( M N P Q ) .
From above we have the side-lengths of the rectangle so evaluating its area is just a matter of calculations: S green = P Q . Q M = B Q . Q M = 2 sin 7 2 π ( 4 sin 7 2 π sin 7 π + 2 cos 7 3 π + 1 ) S green = 8 sin 2 7 2 π sin 7 π + 4 sin 7 2 π cos 7 3 π + 2 sin 7 2 π S green = 4 sin 7 π ( 1 − cos 7 4 π ) + 2 sin 7 − π + 2 sin 7 5 π + 2 sin 7 2 π S green = 4 sin 7 π − 4 sin 7 π cos 7 4 π − 2 sin 7 π + 2 sin 7 2 π + 2 sin 7 2 π S green = 2 sin 7 π − 2 sin 7 − 3 π − 2 sin 7 5 π + 4 sin 7 2 π S green = 2 sin 7 π + 2 sin 7 3 π − 2 sin 7 2 π + 4 sin 7 2 π S green = 2 sin 7 π + 2 sin 7 2 π + 2 sin 7 3 π Finally we have to evaluate the area of the original octadecagon S : S = 6 S cyan + 2 S yellow + 2 S red + S green Substituting and simplifying gives: S = 6 sin 7 π + 3 sin 7 2 π + 1 1 sin 7 3 π Therefore the answer is 6 ∗ 3 ∗ 1 1 = 1 9 8 .
Consider a quarter of the cyan polygon. The angles between the sides and the horizontal are as shown. Split the area into a to g , then we have:
a b = 2 1 ( cos 1 4 π + cos 1 4 5 π + cos 1 4 π + cos 1 4 3 π ) = 2 1 sin 7 π + 2 1 sin 7 2 π + sin 7 3 π = sin 1 4 π ( cos 1 4 5 π + cos 1 4 π + cos 1 4 3 π ) = cos 1 4 6 π cos 1 4 5 π + sin 1 4 π cos 1 4 π + cos 1 4 6 π cos 1 4 3 π = 2 1 ( cos 1 4 π + cos 1 4 1 1 π ) + 2 1 sin 7 π + 2 1 ( cos 1 4 3 π + cos 1 4 9 π ) = 2 1 sin 7 3 π − 2 1 sin 7 2 π + 2 1 sin 7 π + 2 1 sin 7 2 π − 2 1 sin 7 π = 2 1 sin 7 3 π Note that sin θ = cos ( 2 π − θ ) and cos A cos B = 2 1 ( cos ( A − B ) + cos ( A + B ) ) also sin ( 2 θ ) = 2 sin θ cos θ
c = ( sin 1 4 5 π − sin 1 4 π ) ( cos 1 4 π + cos 1 4 3 π ) = ( cos 1 4 2 π − cos 1 4 6 π ) ( cos 1 4 π + cos 1 4 3 π ) = 2 1 ( cos 1 4 π + cos 1 4 3 π + cos 1 4 π + cos 1 4 5 π − cos 1 4 5 π − cos 1 4 7 π 0 − cos 1 4 3 π − cos 1 4 9 π ) = 2 1 sin 7 π + sin 7 3 π
d = 2 1 sin 1 4 3 π cos 1 4 3 π = 4 1 sin 7 3 π , e = g = 4 1 sin 7 π , and f = 4 1 sin 7 5 π = 4 1 sin ( π − 7 5 π ) = 4 1 sin 7 2 π . Therefore the area of the polygon:
A p o l y g o n = 4 ( a + b + c + d + e + f + g ) = 4 ( ( 2 1 + 2 1 + 4 1 + 4 1 ) sin 7 π + ( 2 1 + 4 1 ) sin 7 2 π + ( 1 + 2 1 + 1 + 4 1 ) sin 7 3 π ) = 4 ( 2 3 sin 7 π + 4 3 sin 7 2 π + 4 1 1 sin 7 3 π ) = 6 sin 7 π + 3 sin 7 2 π + 1 1 sin 7 3 π
Therefore A B C = 6 × 3 × 1 1 = 1 9 8 .