One problem leads to another!
Calculus
Level
pending
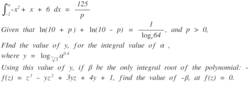 This problem combines calculus and polynomials. Good luck!
This problem combines calculus and polynomials. Good luck!
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we find the value of p. We get: -
\ln { (100\quad -\quad { p }^{ 2 } } )\quad =\quad \ln { \quad 64 } \ 100\quad -\quad { p }^{ 2 }\quad =\quad 64\ { p }^{ 2 }\quad =\quad 36\ p\quad =\quad \pm 6 But p > 0, so p = 6. Now we simplify the integral.
\int _{ -2 }^{ \alpha }{ { -x }^{ 2 } } +\quad x\quad +\quad 6dx\quad =\quad \frac { 125 }{ 6 } \ \begin{matrix} \alpha \ -2 \end{matrix}\left[ \frac { { -x }^{ 3 } }{ 3 } \quad +\quad \frac { { x }^{ 2 } }{ 2 } \quad +\quad 6x \right] \quad =\quad \frac { 125 }{ 6 } \ \left[ \frac { { -\alpha }^{ 3 } }{ 3 } \quad +\quad \frac { { \alpha }^{ 2 } }{ 2 } \quad +\quad 6\alpha \right] -\left[ \frac { 8 }{ 3 } +\quad 2\quad -\quad 12\quad \right] \quad =\quad \frac { 125 }{ 6 } \ \frac { { -2\alpha }^{ 3 }\quad +\quad { 3\alpha }^{ 2 }\quad +\quad 36\alpha }{ 6 } \quad =\quad \frac { 125 }{ 6 } -\quad \frac { 22 }{ 3 } \ \frac { { -2\alpha }^{ 3 }\quad +\quad { 3\alpha }^{ 2 }\quad +\quad 36\alpha }{ 6 } \quad =\quad \frac { 81 }{ 6 } \ { -2\alpha }^{ 3 }\quad +\quad { 3\alpha }^{ 2 }\quad +\quad 36\alpha \quad -\quad 81\quad =\quad 0\
After solving the cubic equation, we get α = 3 or 4.5. As mentioned in the question, y has to be found only for integral values of α, so we substitute α = 3, to get the value of y as 6. Then we find f(z).
f(z)\quad =\quad { z }^{ 3 }\quad -\quad 6{ z }^{ 2 }\quad +\quad 18z\quad +\quad 25\quad =\quad 0\ By\quad factor\quad theorem,\quad (z\quad +\quad 1)\quad is\quad a\quad factor\quad of\quad the\quad polynomial.\ Dividing\quad by\quad (z\quad +\quad 1),\quad we\quad get:\quad -\quad \ (z\quad +\quad 1)({ z }^{ 2 }\quad -\quad 7z\quad +\quad 25)\quad =\quad 0\ After\quad solving\quad for\quad z,\quad we\quad get\quad \beta \quad =\quad -1\quad as\quad the\quad only\quad integral\quad root.\quad \ Therefore,\quad the\quad answer\quad is\quad -(\beta )\quad =\quad \boxed { 1 } \quad \