One side for you, one side for me

Let $R$ be rectangle $ABCD$ such that $A$ and $D$ are vertices on the radius $4$ circle, $B$ and $C$ are vertices on the radius $3$ circle, $O$ is the center of both circles, $\theta = \angle COD$ , $x = AB = CD$ , and $y = AD = BC$ .

The area of rectangle $R$ is $A_R = xy$ . By symmetry, the height of $\triangle OCD$ is $h_{\triangle OCD} = \frac{1}{2}y$ , so its area is $A_{\triangle OCD} = \frac{1}{4}xy$ . The area of $\triangle OCD$ is also $A_{\triangle OCD} = \frac{1}{2} \cdot 3 \cdot 4 \cdot \sin \theta$ . Solving all these equations gives $A_R = 24 \sin \theta$ .

Since $\sin \theta$ has a maximum of $1$ when $\theta = 90°$ , $A_R$ has a maximum of $24$ when $\theta = 90°$ .

By Pythagorean's Theorem on $\triangle OCD$ , $x = 5$ , and since $A_R = xy, y = \frac{24}{5}$ , which means $x - y = 5 - \frac{24}{5} = \frac{1}{5}$ , so $a = 1$ and $b = 5$ , and $a + b = \boxed{6}$ .

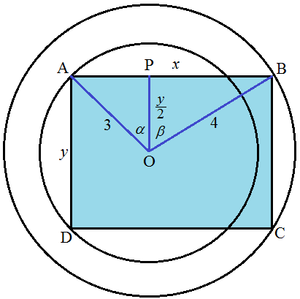
Let the center of the two circles be $O$ and the rectangle be $ABCD$ . The figure shows the arrangement for a larger rectangle. We note that the area of $\triangle OAB$ is $\frac 14$ of the area of the rectangle. Let $OP= \frac y2$ be perpendicular to $AB$ , $\angle AOP = \alpha$ , and $\angle BOP = \beta$ . Since area of $\triangle OAB$ , $[OAB] = \frac 12(3)(4) \sin (\alpha+\beta)$ , it only depends on $\sin(\alpha+\beta)$ , likewise the area of rectangle, $[ABCD] = xy$ is directly proportional to $\sin(\alpha+\beta)$ . And the maximum $\sin(\alpha+\beta)$ is 1, when $\alpha+\beta = 90^\circ$ . When $\alpha+\beta = 90^\circ$ , $\triangle AOP$ is similar to $\triangle BOP$ and $\angle OBP = \angle AOP = \alpha$ . Then we have:

$\begin{aligned} \cos \angle AOP & = \cos \alpha = \frac y6 \\ \sin \angle OBP & = \sin \alpha = \frac y8 \\ \implies \tan \alpha & = \frac 34 & \small \color{#3D99F6} \implies \sin \alpha = \frac 35, \ \cos \alpha = \frac 45 \\ y & = 6 \cos \alpha = \frac {24}5 \\ x & = 3 \sin \alpha + 4 \cos \alpha = 5 \\ \implies x - y & = \frac 15 \end{aligned}$

Therefore, $a+b = 1+5 = \boxed 6$ .

Realizing that the shape has to have a symmetry dividing the rectangle in half along a line passing through the center and parallel to one of the edges, the area is $2 y \left(\sqrt{3^2-y^2}+\sqrt{4^2-y^2}\right)$ . Taking the derivative of the area, setting the derivative to zero and solving for the inflection point, gives the sides of the rectangle: $\left\{2 x,\sqrt{3^2-x^2}+\sqrt{4^2-x^2}\right\}\text{/.}\, \text{Solve}\left[\frac{\partial \left(2 x \left(\sqrt{3^2-x^2}+\sqrt{4^2-x^2}\right)\right)}{\partial x}=0\right] \Longrightarrow \left( \begin{array}{cc} -\frac{24}{5} & 5 \\ \frac{24}{5} & 5 \\ \end{array} \right)$ . Using the positive solution and realizing that $\frac{24}{5}$ is less than $5$ , $\text{With}\left[\left\{\text{result}=5-\frac{24}{5}\right\},\text{Denominator}[\text{result}]+\text{Numerator}[\text{result}]\right] \Longrightarrow 6$ .