One step further.

We will solve it using geometrical probability:

Our desired outcome lies in a sixteenth of a 4-dimensional sphere and all outcomes lie in a 4-dimensional cube so our probability is the hypervolume volume of the sphere over 16 times the hypervolume of the cube. Which is:

$\frac {1}{16} \frac {1^4 \times \frac {π^{2}}{2}}{1^{4}} = \boxed {0.308}$

BTW The hypervolume of a 4D sphere with radius $r$ is given by $r^{4} \times \frac {π^{2}}{2}$ . I've derived this formula by realising that:

$f_{n+1}(r) = \int_{-r}^r\ f_{n}(\sqrt{r^{2}-x^{2}}) dx$

Where $f_{n}(r)$ is the hypervolume of an n-dimensional sphere with radius $r$ .

$f_{0}(1)=1$ because 0-dimensional sphere has one point.

Just to let you guys know the probability after integrating comes out to be

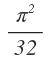
It's possible to generalize this kind of probability problems using geometrical probability: if we have $a_1, a_2,...a_n$ uniformly chosen from $[0,b]$ , the probability of $S=\displaystyle \sum_{i=1}^{n} {a_i}^2 < b^2$ is the probability that point $P=(a_1,...,a_n)$ is inside the origin-centered $n$ -dimensions sphere with radius $b$ . We can express the value of this probability as

$\displaystyle \mathbb{P}(P \subset S)= \frac{1}{b^n}\int_{0}^{b} \int_{0}^{s_2} \int_{0}^{s_3} \dots \int_{0}^{s_n} da_1 da_2...da_n$

where

$\displaystyle s_i=\sqrt{b^2-\sum_{k=1}^{i-1} {a_k}^2}$ .

In our case $n=4$ , $b=1$ so

$\displaystyle \mathbb{P}(P \subset S)= \int_{0}^{b} \int_{0}^{\sqrt{1-{a_1}^2}} \int_{0}^{\sqrt{1-{a_1}^2-{a_2}^2}} \int_{0}^{\sqrt{1-{a_1}^2-{a_2}^2-{a_3}^2}} da_1 da_2 da_3 da_4 \approx \boxed{0.308}$