One theorem to rule them all... do you know what it is?
ABC is a triangle where AC is of length 13, and AB is of length 15. Point D is constructed on side CB such that the ratio C D : D B = 2 1 . Let the cevian AD be of length 6. If CD can be expressed as 6 a , find a .
The answer is 455.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I used the cosines rule :p :p
Log in to reply
Not a bad approach, considering that's what Stewart's Theorem is based on. :D
Log in to reply
Yeah, Stewart's theorem is derived from Cosine Rules. Solving using Cosine Rules is a more original approach to the problem.
Stewarts theorem
Let the ratio be x:2x Then we all have to do is put cosine law for theta and pie-theta.. Add the equations to become zero and then find the value of x.. It comes x^2 = 455/6
You can use The Stewart's Theorem
Perfect.
draw altitude AH;let CH=m , CD=x; use Pythagorean theorem: A D 2 = A H 2 + H D 2 ; A C 2 = A H 2 + C H 2 ; =>(AC-AD)(AC+AD)=(CH-HD)(CH+HD) ; =>133=(2m-x)x=>133=2mx- x 2 =>399=6mx-3 x 2 (1 ) ; do the same thing with AC and AB =>56=(3x-2m)3x=>56=9 x 2 -6mx (2 ) ; plus (1 ) with (2 ) =>455=6 x 2 => x 2 =455/6 .
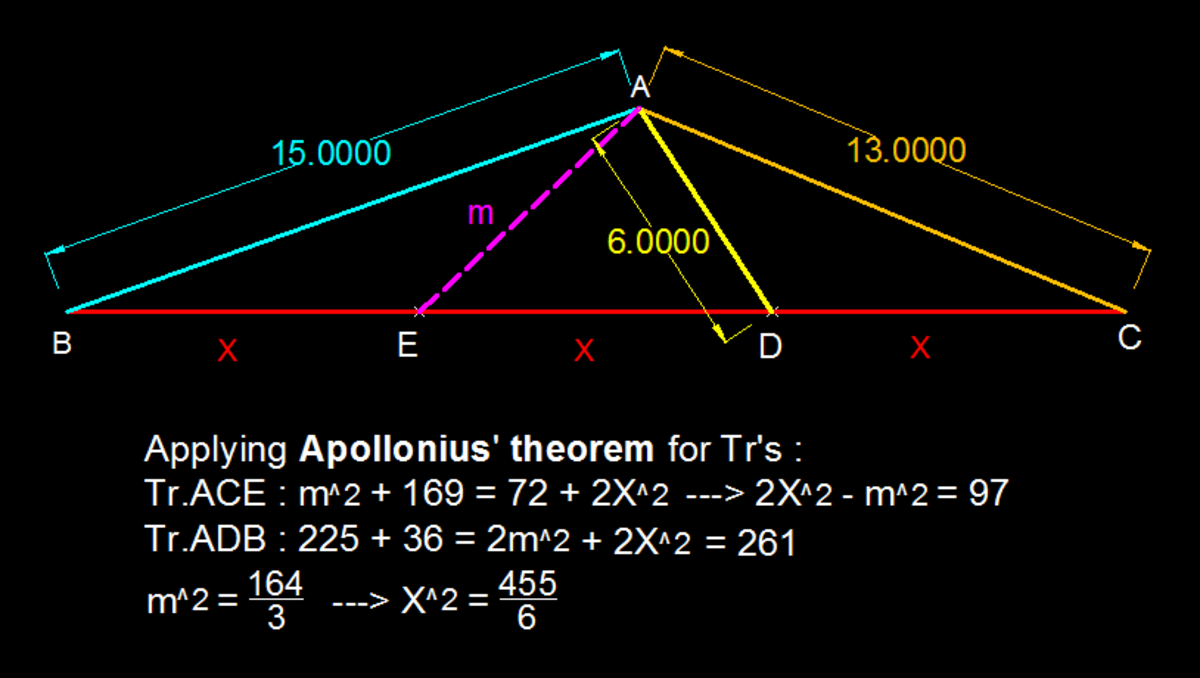
The "One Theorem to Rule Them All" is Stewart's Theorem. It is a relatively complex formula that is really nifty to hold on to. By letting CD be x , and DB be 2 x , plugging that into the formula produces x 2 = 6 4 5 5 . Thus a = 4 5 5 . It's a really nifty theorem that I have seen on tons of AIME problems. :D