All The Numbers Are Connected!
If each of the missing numbers in the blanks is a single-digit number, what is the sum of all the missing numbers?
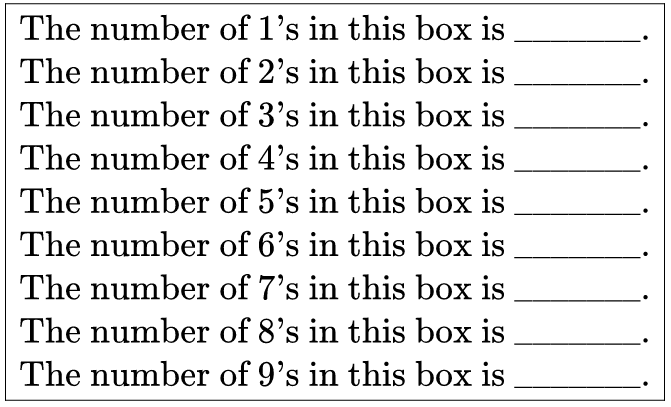
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How did you find out that procedure?
Log in to reply
Note that it is not necessary to find the correct configuration to solve the problem though as you can find that sum by other ways as well anyway.
Because the numbers which you insert in the blanks describes the number of times each number repeats and the number of repeats of this numbers is limited by the number of apparitions of the numbers in the box giving a total of 9+9=18 the sum of the numbers in the blank spaces is a priori 18 anyway.
Right but can you should describe the procedure by which you arrived at the result or some guiding steps that made you arrive at the configuration and justify it's uniqueness so that it is explicitly made obvious that there is no other possible working configuration for this problem anyway.
Maybe your title is a good point to start your explanation of how to arrive at a configuration which is solid and logically sound or in other words non-contradictory and can give some insight in understanding this sort of problem better anyway.
There are 9 statements each containing 2 digits (note each blank is filled by a single digit number). Thus there are 18 digits total, so the sum is 1 8 .
Can you please clarify?
Log in to reply
These numbers count the total number of 1s, 2s, etc. in the box, so their sum is the total number of numbers in the box. But we are told there are 9 single digits here, so there are 18 numbers total, so the sum must be 18.
10+1+1+1+1+1+1+1+1+1 Since there was no restrictions on 0 There are 10 1s including the one in the statement.
i am sorry, i missed that detail of single digit numbers
Your solution does work, however the question states that all numbers n the box are single digits. So the actual answer is 6+3+2+1+1+2+1+1+1=18.
Let's start with this: The number of 1’s in this box is The number of 2’s in this box is The number of 3’s in this box is The number of 4’s in this box is The number of 5’s in this box is The number of 6’s in this box is The number of 7’s in this box is The number of 8’s in this box is The number of 9’s in this box is _____ _____ _____ _____ _____ _____ _____ _____ _____
So the first thing to do is to just do the question without considering the actual answers themselves:
The number of 1’s in this box is The number of 2’s in this box is The number of 3’s in this box is The number of 4’s in this box is The number of 5’s in this box is The number of 6’s in this box is The number of 7’s in this box is The number of 8’s in this box is The number of 9’s in this box is 1 1 1 1 1 1 1 1 1
Ok, but we now have a total of 10 1's in the box. We could put in 10 as the number of 1's, but the question specifies that only single digits are allowed. So we'll do this for now:
The number of 1’s in this box is The number of 2’s in this box is The number of 3’s in this box is The number of 4’s in this box is The number of 5’s in this box is The number of 6’s in this box is The number of 7’s in this box is The number of 8’s in this box is The number of 9’s in this box is 9 1 1 1 1 1 1 1 2
Now, you can see that there are 2 twos in the box and if we put a 2 in the twos section we'll get three twos and therefore two threes, like so:
The number of 1’s in this box is The number of 2’s in this box is The number of 3’s in this box is The number of 4’s in this box is The number of 5’s in this box is The number of 6’s in this box is The number of 7’s in this box is The number of 8’s in this box is The number of 9’s in this box is 9 3 2 1 1 1 1 1 2
And now we can see that there are only 6 1's left, so we can just move the 2 that's in the 9's spot:
The number of 1’s in this box is The number of 2’s in this box is The number of 3’s in this box is The number of 4’s in this box is The number of 5’s in this box is The number of 6’s in this box is The number of 7’s in this box is The number of 8’s in this box is The number of 9’s in this box is 6 3 2 1 1 2 1 1 1
Now you can see that everything holds without descending to chaos, as was not the case with quite a few people who tried to solve this problem i.e. my classmates.
And 6 + 3 + 2 + 1 + 1 + 2 + 1 + 1 + 1 = 1 8