One to Two,Isosceles to Isosceles
One possible way to draw
A
B
C
and split it into two isosceles triangles is shown here.
An isosceles triangle A B C ( with ∠ B = ∠ C ) is cut into two smaller isosceles triangles (which don't have to be identical).
How many different possible angles ∠ A are there?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Ergh. I read the question as asking , for some A, how many other angles in the diagram had the same value
Log in to reply
Same. It would be 3, right?
Log in to reply
Same here as well. And yes, it would be 3.
Yea, I got three. This one is way over my head.
the authors!! PLEASE change the text! the way it is now, especially those unnoticeable small letters under the drawing, is quite misleading and bloody irritating! my advise is to put the phrase "one possible way to..." RIGHT BEFORE the question, so it was much more distinctive!
WHAT A SMALL SOLUTION.
Log in to reply
Lol..😂😄😅. I've never seen such a small solution!
There has to be a simpler solution. I obviously missed something in my approach and only found two but wasn't expecting this. I'm still none the wiser, apart from realising that I missed the right-angle triangle solution.
Thanks for telling me that this question is indeed not so easy to me...
Help
Take and c to be x Then angle b=x Angle BDC =x This makes angle ABD=3x-180 Angle a =180-2x As both are equal x=72
Now this is what I call a SOLUTION!
I'll pretend i get it 🙄
How do you have patience to write such a long answer??
Label the angles as follows:
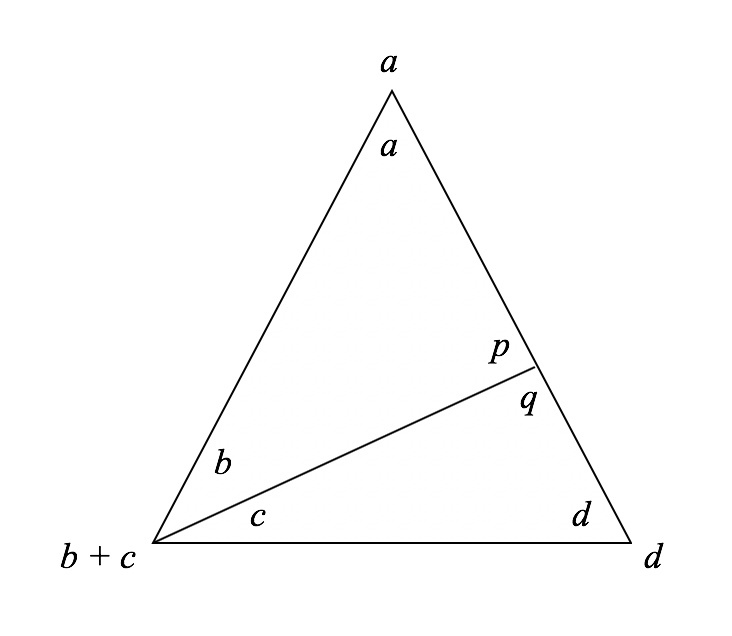
The angles satisfy the equations ⎩ ⎪ ⎨ ⎪ ⎧ a + b = q c + d = p a + b + c + d = p + q = 1 8 0 ∘
Now consider the different cases, based on which angles are equal in the three triangles. In each triangle there are potentially three angles that could be the vertex angle, making for 27 cases in principle; but several of them can be ruled out, because
-
a or d cannot be the vertex angle in both the large and a small triangle;
-
if b + c is the vertex angle in the large triangle, neither b nor c can be the vertex angle in the smaller triangles;
-
if d is the vertex angle in the large triangle, p cannot be the vertex angle in a small triangle; the same holds for a and q ;
-
the symmetry between ( a , b , p ) and ( c , d , q ) allows us to rule out some more cases.
-
That leaves the following cases
case ( 1 ) ( 2 ) ( 3 ) ( 4 ) ( 5 ) ( 6 ) ( 7 ) large triangle a = d a = d a = d a = b + c a = b + c a = b + c a = b + c small triangle 1 a = b a = b b = p a = p a = p b = p b = p small triangle 2 c = d c = q c = q c = d d = q c = d d = q
For each case, we substitute the given values into the three equations listed at the beginning. We obtain:
-
Case (1): a = b = c = d , 4 a = 1 8 0 ∘ , a = 4 5 ∘ , vertex angle b + c = 9 0 ∘ .
-
Case (2): a = b = d , 3 a + c = 1 8 0 ∘ , (2a = c), 5 a = 1 8 0 ∘ , a = 3 6 ∘ , vertex angle b + c = 3 a = 1 0 8 ∘ .
-
Case (3): a = d , a + b = c , c + a = b , which gives a = 0 , which is impossible.
-
Case (4): b = c = d , a = 2 c , 5 c = 1 8 0 ∘ , c = 3 6 ∘ , vertex angle d = c = 3 6 ∘ .
-
Case (5): b = d = a + b , so that a = 0 , which is impossible.
-
Case (6): a = 3 c , b = p = 2 c , q = 5 c , 7 c = 1 8 0 ∘ , vertex angle d = c = 2 5 7 5 ∘ .
-
Case (7): a = p + c = 2 c + d = 2 c + a + b , so that 2 c + b = 0 , which is impossible.
Thus we see that there are four possible vertex angles for the large triangle.
A picture/diagram would be helpful to understand it better.
The 4 different ∠ A possibilities are ∠ A = 1 0 8 ° , ∠ A = 9 0 ° , ∠ A = 2 5 7 5 ° , and ∠ A = 3 6 ° , as illustrated below:
In order to make 2 triangles out of 1 triangle from one cut, the cut must go through a vertex and its opposite side. Since △ A B C is an isosceles with ∠ B = ∠ C , so we only need to consider cuts that go through either ∠ A or ∠ B . In all cases, A B = B C and ∠ B = ∠ C by isosceles triangle properties.
Case A : Let the cut intersect ∠ A and point D along B C . If the cut results in 2 isosceles triangles, then there are 9 cases to consider:
A 1 ) A B = A D and A D = A C . Let x = ∠ C . Then ∠ A D C = x since A D = A C , ∠ A D B = 1 8 0 ° − x since ∠ A D C and ∠ A D B are linear, ∠ A B D = 1 8 0 ° − x since A B = A D , so x = 1 8 0 ° − x since ∠ B = ∠ C , which means x = 9 0 ° , which means △ A C D has two right angles, which is not possible.
A 2 ) A B = A D and A D = C D . Let x = ∠ C . Then ∠ C A D = x since A D = D C , ∠ A D C = 1 8 0 ° − 2 x by triangle sum of △ A C D , ∠ A D B = 2 x since ∠ A D C and ∠ A D B are linear, ∠ B = 2 x since A B = A D , so x = 2 x since ∠ B = ∠ C , which means x = 0 ° , which is not a possible angle for a triangle.
A 3 ) A B = A D and A C = C D . Let x = ∠ C . Then ∠ A D C = 9 0 ° − 2 x by isosceles triangle sum of △ A C D , ∠ A D B = 9 0 ° + 2 x since ∠ A D C and ∠ A D B are linear, ∠ B = 9 0 ° + 2 x since A B = A D , so x = 9 0 ° + 2 x since ∠ B = ∠ C , which means x = 1 8 0 ° , which is not a possible angle for a triangle.
A 4 ) A B = B D and A D = A C . By symmetry this is the same as Case A 3 , which was not possible.
A 5 ) A B = B D and A D = C D . Let x = ∠ C . Then ∠ C A D = x since A D = D C , ∠ A D C = 1 8 0 ° − 2 x by triangle sum of △ A C D , ∠ A D B = 2 x since ∠ A D C and ∠ A D B are linear, ∠ B A D = 2 x since A B = B D , ∠ B = 1 8 0 ° − 4 x by triangle sum of △ A C D , so x = 1 8 0 ° − 4 x since ∠ B = ∠ C , which means x = 3 6 ° , ∠ C A D = x = 3 6 ° , ∠ B A D = 2 x = 2 ⋅ 3 6 ° = 7 2 ° , and ∠ A = ∠ B A D + ∠ C A D = 7 2 ° + 3 6 ° = 1 0 8 ° .
A 6 ) A B = B D and A C = C D . Let x = ∠ C . Then ∠ A D C = 9 0 ° − 2 x by isosceles triangle sum of △ A C D , ∠ A D B = 9 0 ° + 2 x since ∠ A D C and ∠ A D B are linear, ∠ B A D = 9 0 ° + 2 x since A B = A D , ∠ B = − x by triangle sum of △ A B D , so x = − x since ∠ B = ∠ C , which means x = 0 ° , which is not a possible angle for a triangle.
A 7 ) A D = B D and A D = A C . By symmetry this is the same as Case A 2 , which was not possible.
A 8 ) A D = B D and A D = C D . Let x = ∠ C . Then ∠ C A D = x since A D = D C , ∠ A D C = 1 8 0 ° − 2 x by triangle sum of △ A C D , ∠ A D B = 2 x since ∠ A D C and ∠ A D B are linear, ∠ B = ∠ B A D = 9 0 ° − x by isosceles triangle sum of △ A B D , so x = 9 0 ° − x since ∠ B = ∠ C , which means x = 4 5 ° , ∠ C A D = x = 4 5 ° , ∠ B A D = 9 0 ° − x = 9 0 ° − 4 5 ° = 4 5 ° , and ∠ A = ∠ B A D + ∠ C A D = 4 5 ° + 4 5 ° = 9 0 ° .
A 9 ) A D = B D and A C = C D . By symmetry this is the same as Case A 5 , which would give ∠ A = 1 0 8 ° again.
Case B : Let the cut intersect ∠ B and point D along A C . If the cut results in 2 isosceles triangles, then there are 9 cases to consider:
B 1 ) A B = B D and B C = B D . Let x = ∠ C . Then ∠ B D C = x since B C = B D , ∠ A D B = 1 8 0 ° − x since ∠ B D C and ∠ A D B are linear, ∠ A = 1 8 0 ° − x since A B = B D , ∠ C B D = 1 8 0 ° − 2 x by triangle sum of △ B C D , ∠ A B D = 2 x − 1 8 0 ° by triangle sum of △ A B D , ∠ B = 0 ° as the sum of ∠ C B D and ∠ B C D , which is not a possible angle for a triangle.
B 2 ) A B = B D and B D = C D . Let x = ∠ C . Then ∠ C B D = x since B D = C D , ∠ B D C = 1 8 0 ° − 2 x by triangle sum of △ B C D , ∠ A D B = 2 x since ∠ B D C and ∠ A D B are linear, ∠ A = 2 x since A B = B D , ∠ A B D = 1 8 0 ° − 4 x by triangle sum of △ A B D , ∠ B = 1 8 0 ° − 3 x as the sum of ∠ C B D and ∠ B C D , so x = 1 8 0 ° − 3 x since ∠ B = ∠ C , which means x = 4 5 ° , ∠ A D B = 2 x = 2 ⋅ 4 5 ° = 9 0 ° , and ∠ A = 2 x = 2 ⋅ 4 5 ° = 9 0 ° , which means △ A B D has two right angles, which is not possible.
B 3 ) A B = B D and B C = C D . Let x = ∠ C . Then ∠ C B D = ∠ C D B = 9 0 ° − 2 x by isosceles triangle sum of △ B C D , ∠ A D B = 9 0 ° + 2 x since ∠ B D C and ∠ A D B are linear, ∠ A = 9 0 ° + 2 x since A B = B D , ∠ A B D = − x by triangle sum of △ A B D , ∠ B = 9 0 ° − 2 3 x as the sum of ∠ C B D and ∠ B C D , so x = 9 0 ° − 2 3 x since ∠ B = ∠ C , which means x = 7 2 ° and ∠ A B D = − x = − 7 2 ° , which is not a possible angle for a triangle.
B 4 ) A D = B D and B C = B D . Let x = ∠ C . Then ∠ B D C = x since B C = B D , ∠ A D B = 1 8 0 ° − x since ∠ B D C and ∠ A D B are linear, ∠ C B D = 1 8 0 ° − 2 x by triangle sum of △ B C D , ∠ A = ∠ A B D = 2 x by isosceles triangle sum of △ A B D , ∠ B = 1 8 0 ° − 2 3 x as the sum of ∠ C B D and ∠ B C D , so x = 1 8 0 ° − 2 3 x since ∠ B = ∠ C , which means x = 7 2 ° and ∠ A = 2 x = 2 7 2 ° = 3 6 ° .
B 5 ) A D = B D and B D = C D . Let x = ∠ C . Then ∠ C B D = x since B D = C D , ∠ B D C = 1 8 0 ° − 2 x by triangle sum of △ B C D , ∠ A D B = 2 x since ∠ B D C and ∠ A D B are linear, ∠ A = ∠ A B D = 9 0 ° − x by isosceles triangle sum of △ A B D , ∠ B = 9 0 ° as the sum of ∠ C B D and ∠ B C D , so x = 9 0 ° since ∠ B = ∠ C , which means ∠ B = ∠ C = 9 0 ° , which means △ A B C has two right angles, which is not possible.
B 6 ) A D = B D and B C = C D . Let x = ∠ C . Then ∠ C B D = ∠ C D B = 9 0 ° − 2 x by isosceles triangle sum of △ B C D , ∠ A D B = 9 0 ° + 2 x since ∠ B D C and ∠ A D B are linear, ∠ A = ∠ A B D = 4 5 ° − 4 x by isosceles triangle sum of △ A B D , ∠ B = 1 3 5 ° − 4 3 x as the sum of ∠ C B D and ∠ B C D , so x = 1 3 5 ° − 4 3 x since ∠ B = ∠ C , which means x = 7 7 7 1 ° and ∠ A = 4 5 ° − 4 x = 4 5 ° − 4 7 7 7 1 ° = 2 5 7 5 ° .
B 7 ) A B = A D and B C = B D . Then A C = A B = A D , and C D = A C − A D = 0 , which is not a possible length for a triangle.
B 8 ) A B = A D and B D = C D . Then A C = A B = A D , and C D = A C − A D = 0 , which is not a possible length for a triangle.
B 9 ) A B = A D and B C = C D . Then A C = A B = A D , and C D = A C − A D = 0 , which is not a possible length for a triangle.
Therefore, the only different ∠ A possibilities are 1 0 8 ° , 9 0 ° , 2 5 7 5 ° , and 3 6 ° .